三教科の得点表
x <- "./data/Pre_P20_演習1.csv" %>%
read.csv()
x %>% df_print()本講はテキストの概観に関する第一回講義における演習をRで解答したものです。テキストとは異なるデータを利用しており演習自体やデータの著作権は講義担当者にあります。
グループ演習1（分布の特徴を捉える）
Q1 各教科の得点の違いを考える（演習1）
データの分布傾向を見るには箱ひげ図が便利です。Rで箱ひげ図を描くにはboxplot()関数を用います。
箱ひげ図による得点分布の可視化
boxplot(x)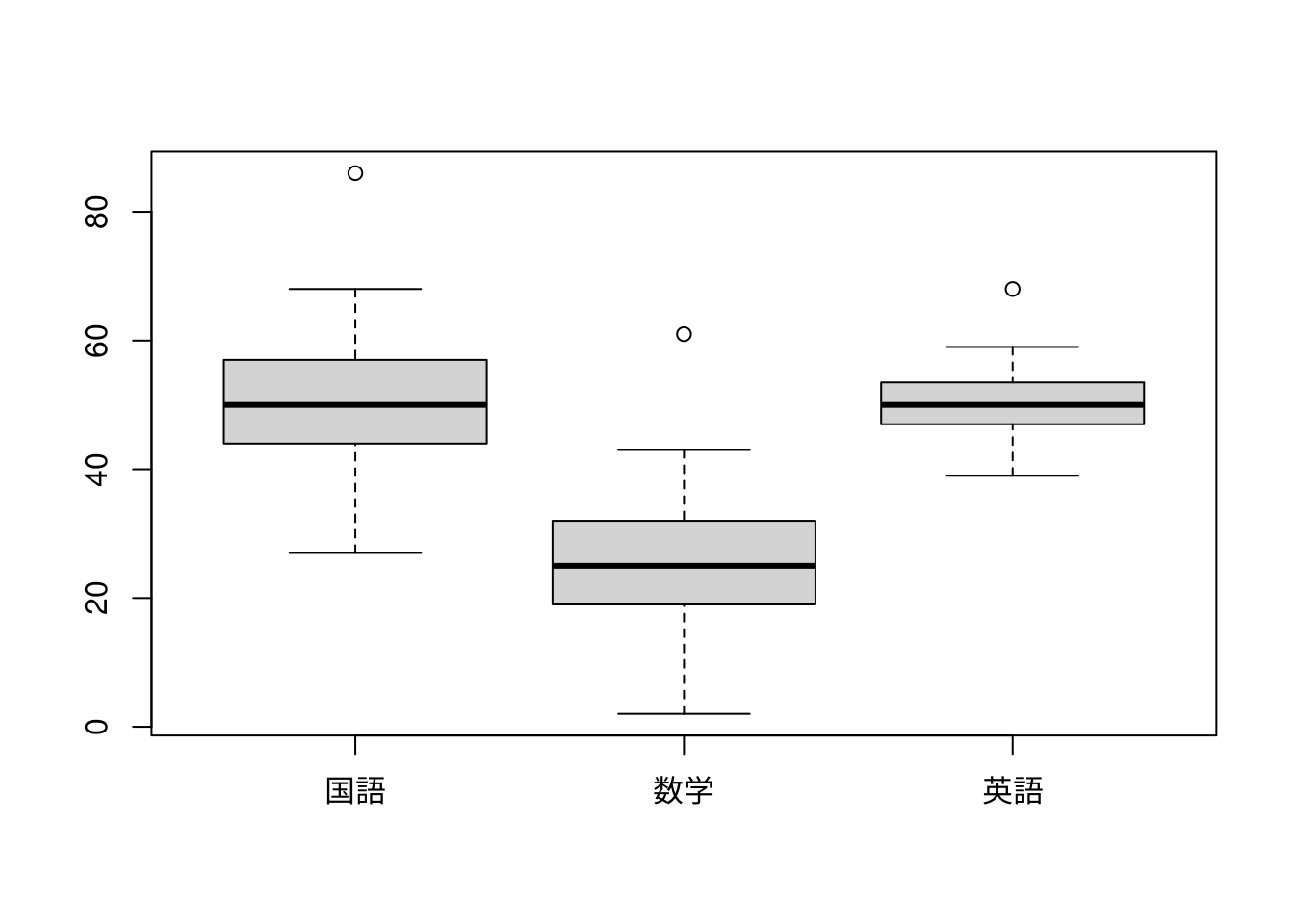
箱ひげ図は五数要約の値を箱とひげ（whisker）で表現したもので、boxplot()関数の場合は外れ値（outliers）が描かれます。五数要約は下表のようなもので、上から最小値、第一四分位値（25%点）、中央値・第二四分位値（50%点）、第三四分位値（75%点）、最大値となっています。
五数要約
x %>%
dplyr::summarise(dplyr::across(.cols = dplyr::everything(),
.fns = fivenum)) %>%
df_print()
箱ひげ図からは以下のような特徴がうかがえます。
- 英語の得点は他の二教科に比べて狭い範囲に得点が集中している
- 数学の得点は他の二教科に比べて全体的に得点が低めである
- 国語の得点は中央値は英語の得点と同じである
- 国語の得点は英語の得点より倍近い範囲に得点が散らばっている
- どの教科も一人は、理解度が高い（高得点な）人がいる
箱ひげ図はデータを要約した結果を図示したものですので、もう少し細かい分布を見るにはヒストグラム（度数分布表）が便利です。Rではhist()関数を用いて描きます。
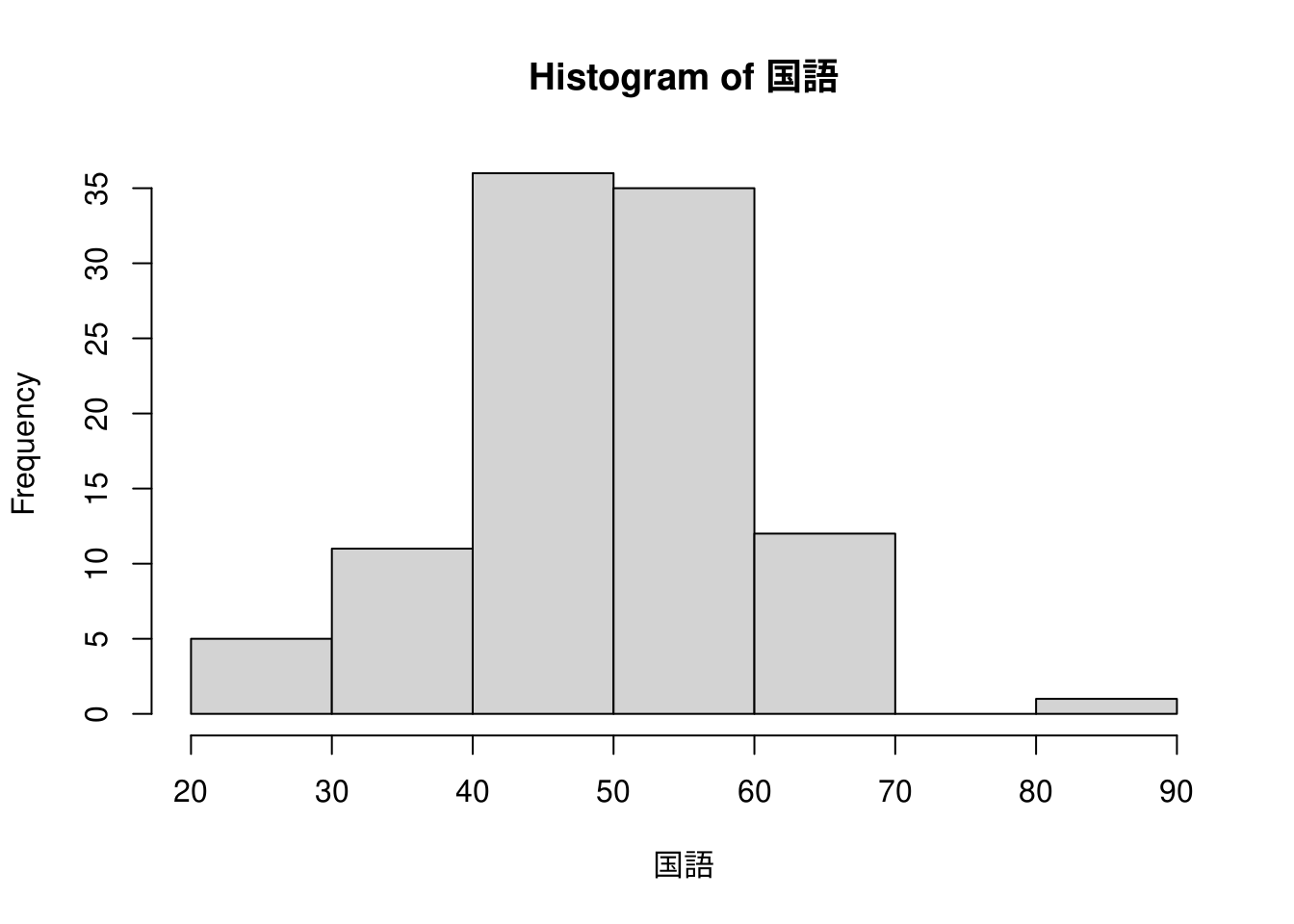
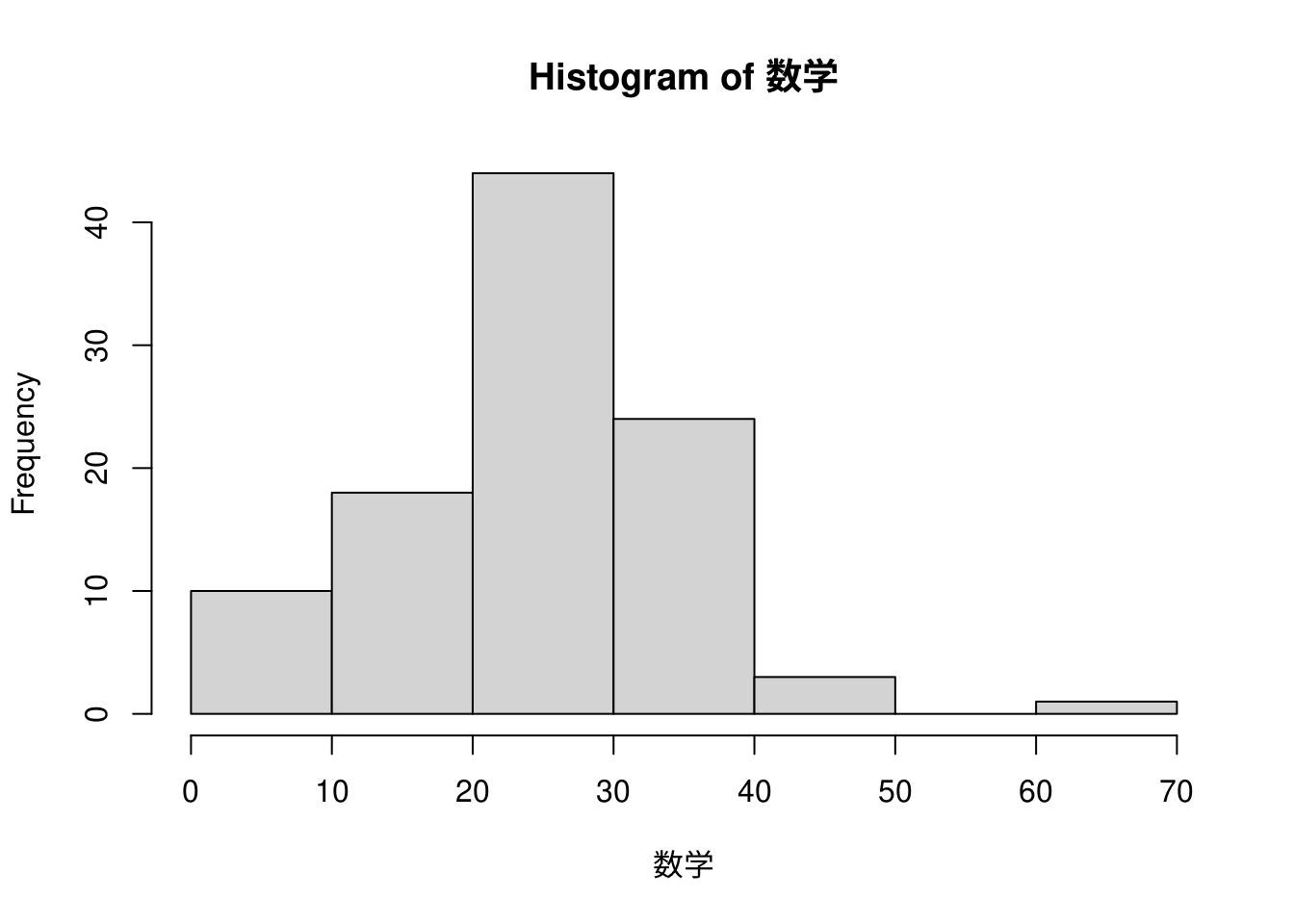
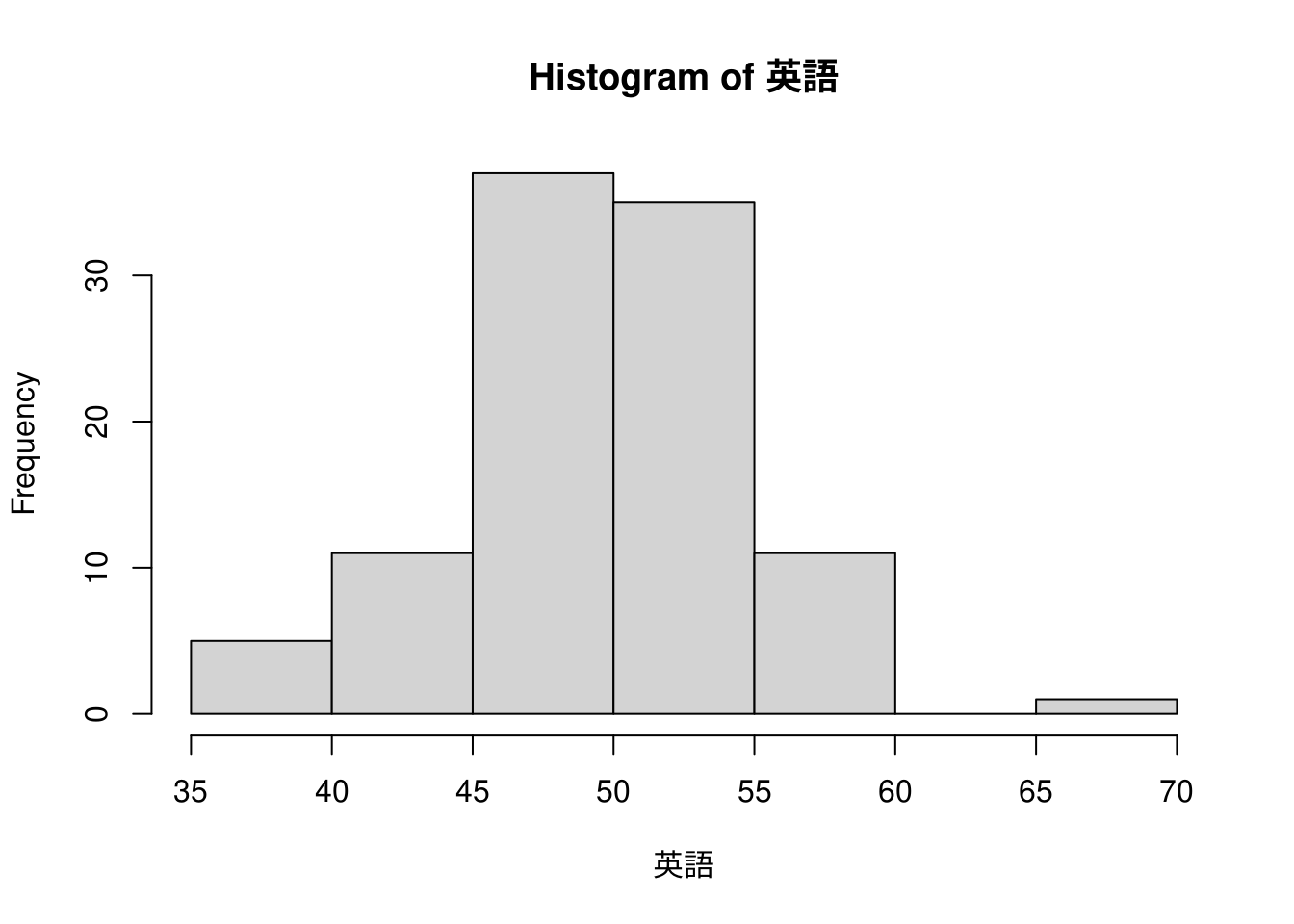
ヒストグラムで見ると以下のような特徴がうかがえます。
- 概ね箱ひげ図でうかがえた特徴通りである
- 国語の得点の7割近くが中央値の付近に集中している
- 英語の得点の7割近くが中央値の付近に集中している
- 英語で得点30点はありえない（このデータでは存在しない）
- 数学の得点は他の二教科にくらべると綺麗な分布をしている
教科間の得点の関係をみるには散布図行列が便利です。Rではpairs()関数が標準関数として用意されていますが、ここではpsychパッケージのpsych::pairs.panels(x)関数を用います。
散布図行列
psych::pairs.panels(x)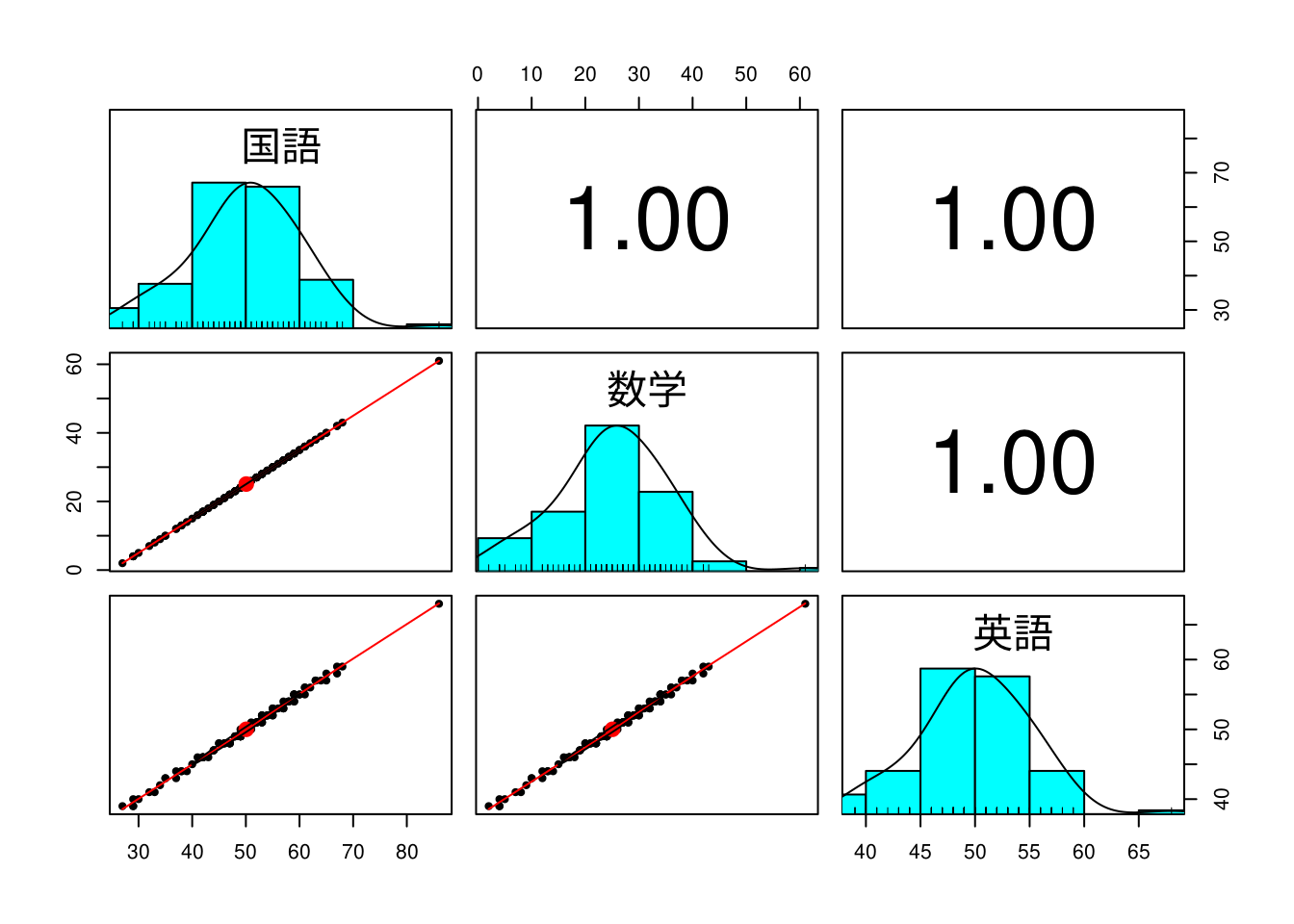
散布図行列で見ると以下のような特徴がうかがえます。
- 不自然なほど教科間に強い相関が認められる
- 人為的な的なデータであることがうかがえる
個人演習（基本統計量の算出）
Q2 基本統計量から違いを考察する（演習1）
グループ演習1のデータを用いて基本統計量を求めます。最初は平均値です。Rで平均値を求めるにはmean()関数を用います。
平均値
x %>%
dplyr::summarise(dplyr::across(dplyr::everything(), mean)) %>%
df_print()
参考として中央値も求めてみます。中央値はmedian()関数で求めます。
中央値
x %>%
dplyr::summarise(dplyr::across(dplyr::everything(), median)) %>%
df_print()
次に分散（母分散）を求めます。Rには母分散を求める関数がありませんので、本資料では計算式（\(\frac{\sum{(x_i - \mu)^2}}{n} = \sigma^2\)）をVAR()関数として定義しています。
（母）分散
x %>%
dplyr::summarise(dplyr::across(dplyr::everything(), VAR)) %>%
round(digits = 1) %>%
df_print()
分散を求めましたので標準偏差（母標準偏差）を求めますが、母分散同様に求める関数がありませんので本資料では計算式（\(\sqrt{\frac{\sum{(x_i - \mu)^2}}{n}} = \sigma\)）をSD()関数として定義しています。
（母）標準偏差
x %>%
dplyr::summarise(dplyr::across(dplyr::everything(), SD)) %>%
round(digits = 1) %>%
df_print()
最後に変動係数（ばらつきを比較するための値）を求めます。
変動係数
x %>%
dplyr::summarise(dplyr::across(dplyr::everything(),
function(x = .) {SD(x)/mean(x)} )) %>%
round(digits = 2) %>%
df_print()
考察
以上の基本統計量より
- 平均値から数学の得点は他の二教科に比べて全体的に得点が低めであることがわかる
- 中央値から三教科とも左右対称な分布をしいていることが推測できる
- 標準偏差から英語の得点が他の二教科に比べて狭い範囲に集中していることがわかる
- 変動係数から数学より国語の方がバラツキが少ないことがわかる
- 変動係数から国語より英語の方がバラツキが少ないことがわかる
したがって
- 国語は他の二教科に比べて理解度にバラツキがあると推測できる
- 英語は他の二教科に比べて理解度にバラツキがないと推測できる
- 数学は他の二教科に比べて理解度が全体的位低い可能性がある
- もしくは難易度が高かった可能性がある
おまけ
基本統計量をまとめて計算するにはskimrパッケージのskimr::skim()関数が便利です。ただし、求められる標準偏差は母標準偏差の推定量です。
基本統計量
skimr::skim(x) %>%
df_print()
個人演習（層別ヒストグラムの作成）
Q3 ヒストグラムを作成して比較する（演習1）
層別のヒストグラムを描くにはggplot2パッケージが便利です。ここでは階級幅を\(10\mbox{点}\)としています。
層別ヒストグラム
x %>%
tidyr::pivot_longer(cols = dplyr::everything(),
names_to = "教科", values_to = "得点") %>%
dplyr::mutate(教科 = forcats::fct_inorder(教科)) %>%
ggplot2::ggplot(ggplot2::aes(x = 得点, fill = 教科)) +
ggplot2::geom_histogram(breaks = seq(0, 100, 10), alpha = 0.5) +
ggplot2::facet_grid(rows = dplyr::vars(教科))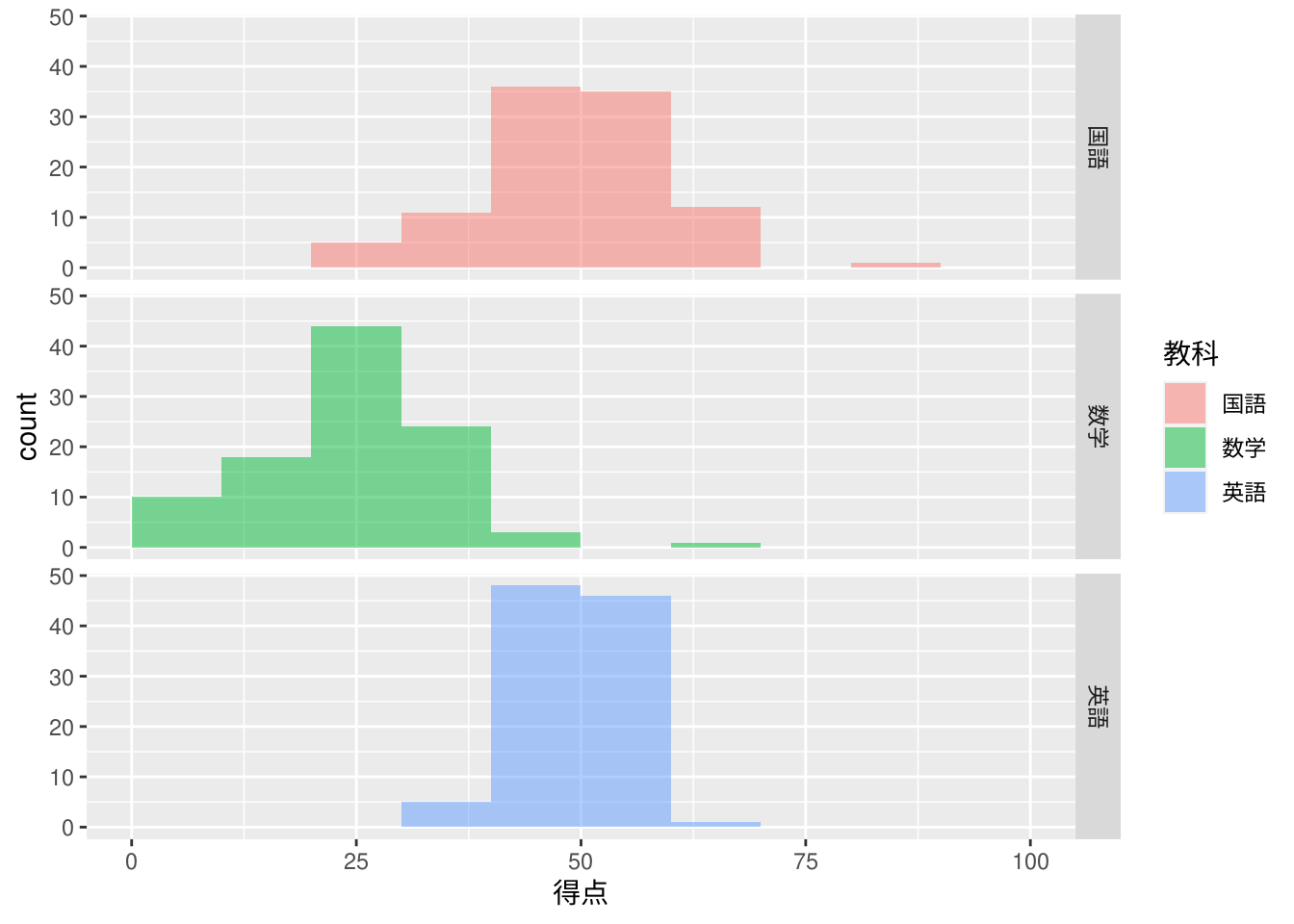
ヒストグラムの調整比較
Microsoft Excel（2016以降）ではヒストグラムを描くことができますが、グラフ表示の調整には制限があります。Excelでヒストグラム間の比較を行いたい場合は小池方式のテクニックを使う必要がありますが、他のツールでは調整が可能です。
| ツール名 | 階級幅 | 階級（横軸） | 度数（縦軸） | 閉じ1 |
|---|---|---|---|---|
| Microsoft Excel(365) | 調整可 | 調整不可 | 調整不可 | 調整不可 |
| Google Spreadsheet | 調整可 | 調整可 | 調整可 | 調整不可 |
| Base R (hist) | 調整可 | 調整可 | 調整可 | 調整可 |
| R/Tidyverse (ggplot2) | 調整可 | 調整可 | 調整可 | 調整可 |
1 閉じとは階級の境界にあたるデータの処理方法です。\(a < x \le b\)を右閉じ、\(a \le x < b\)を左閉じといい、右閉じが主流です。
グループ演習2（同じ30点でも）
| 統計量 | 国語 | 数学 | 英語 | 備考 |
|---|---|---|---|---|
| 平均 | 50 | 25 | 50 | |
| 分散 | 101 | 101 | 26 | 母分散 |
| 標準偏差 | 10 | 10 | 5 | 標準偏差の推定値 |
| 変動係数 | 0.20 | 0.40 | 0.10 | |
| 中央値 | 50 | 25 | 50 | 第二四分位値（参考） |
層別ヒストグラム
x %>%
tidyr::pivot_longer(cols = dplyr::everything(),
names_to = "教科", values_to = "得点") %>%
dplyr::mutate(教科 = forcats::fct_inorder(教科)) %>%
ggplot2::ggplot(ggplot2::aes(x = 得点, fill = 教科)) +
ggplot2::geom_histogram(breaks = seq(0, 100, 10), alpha = 0.5) +
ggplot2::facet_grid(rows = dplyr::vars(教科)) +
ggplot2::geom_vline(xintercept = 30, colour = "red", size = 0.25)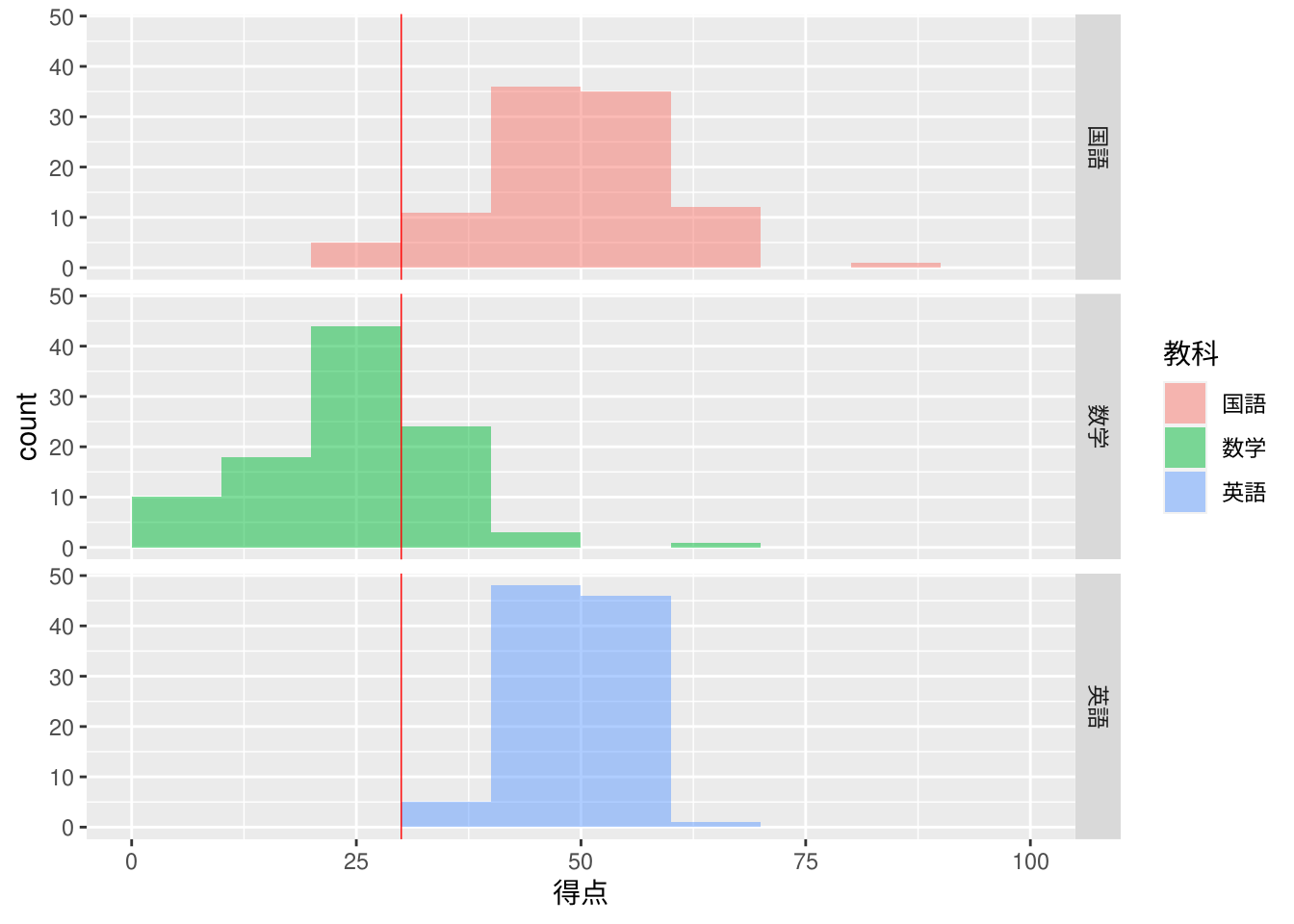
上記より30点という得点は以下のように判断できます。
- 国語は悪い得点
- \(\mu - 2\sigma\)なので
- 数学はまあまあの得点
- \(\mu + 1\sigma\)以内なのですごく良いとは言えない（まあ平均的）
- 英語は非常に悪い得点
- \(\mu - 3\sigma\)の外側なので本来ならありえない（実際データにはない）
また、以下のようなことも推測できます。
- 数学は50点以上の得点を取得したものほぼいないことから難しい問題
- もしくは、全体の理解度が低い
- 英語は標準偏差が他の二教科に比べると小さいので全体の理解度がある程度の水準にある
- もしくは、極端に難しい問題が半分くらいある
個人演習（テスト結果を比べる）
対象データは下記の通り。
三教科の平均点と標準偏差
x <- "./data/Pre_P37_個人演習.csv" %>%
read.csv()
x %>% df_print()
Q1 成績の良い順に並べる（演習2）
Zスコアと偏差値を算出して成績の良い順に並べる。
Zスコアと偏差値を求める
Q2 相対順位を算出する（演習2）
Zスコアから相対順位（上位\(%\))を求める。
相対順位
Q3 SECデータ白書のベンチワーク（演習2）
計算結果
グループ演習3（二群のデータの違いによるp値比較）
4パターンの二群のデータ
x <- "./data/Pre_P53_2群のデータ.csv" %>%
read.csv()
x %>% df_print()4パターンの二群のデータ
"./data/Pre_P52_4パターン.csv" %>%
read.csv() %>%
ggplot2::ggplot(ggplot2::aes(x = Group, y = Value, colour = Group)) +
ggplot2::geom_jitter(position = "dodge") +
ggplot2::facet_grid(~ Pattern)Warning: Width not defined. Set with `position_dodge(width = ?)`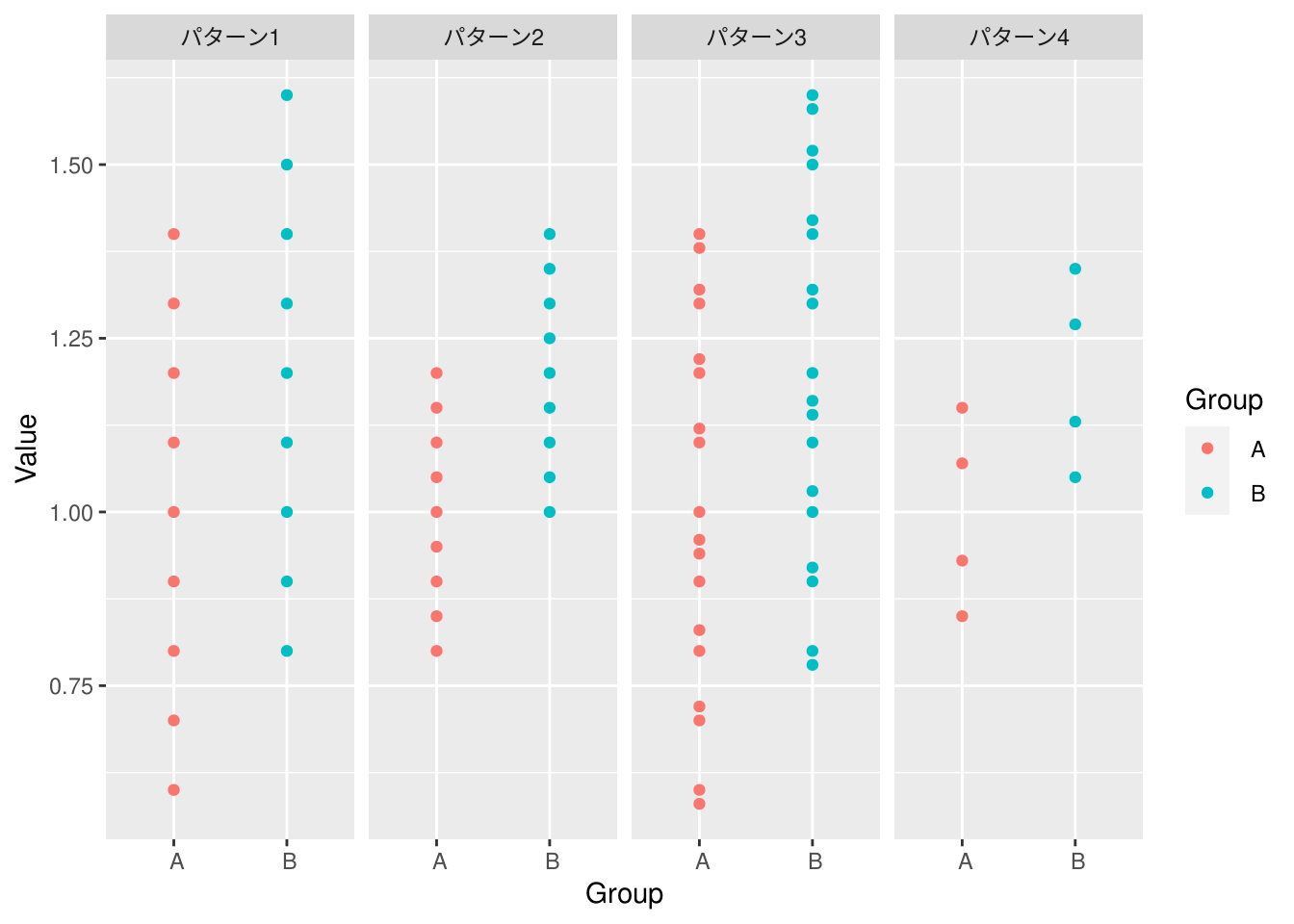
Q1 グラフから結果を予想する（演習3）
グラフから結果を予想するにあたり、データの分布が見やすい箱ひげ図を描いておきます。
4パターンの二群のデータ
"./data/Pre_P52_4パターン.csv" %>%
read.csv() %>%
ggplot2::ggplot(ggplot2::aes(x = Group, y = Value, colour = Group)) +
ggplot2::geom_boxplot(position = "dodge") +
ggplot2::facet_grid(~ Pattern)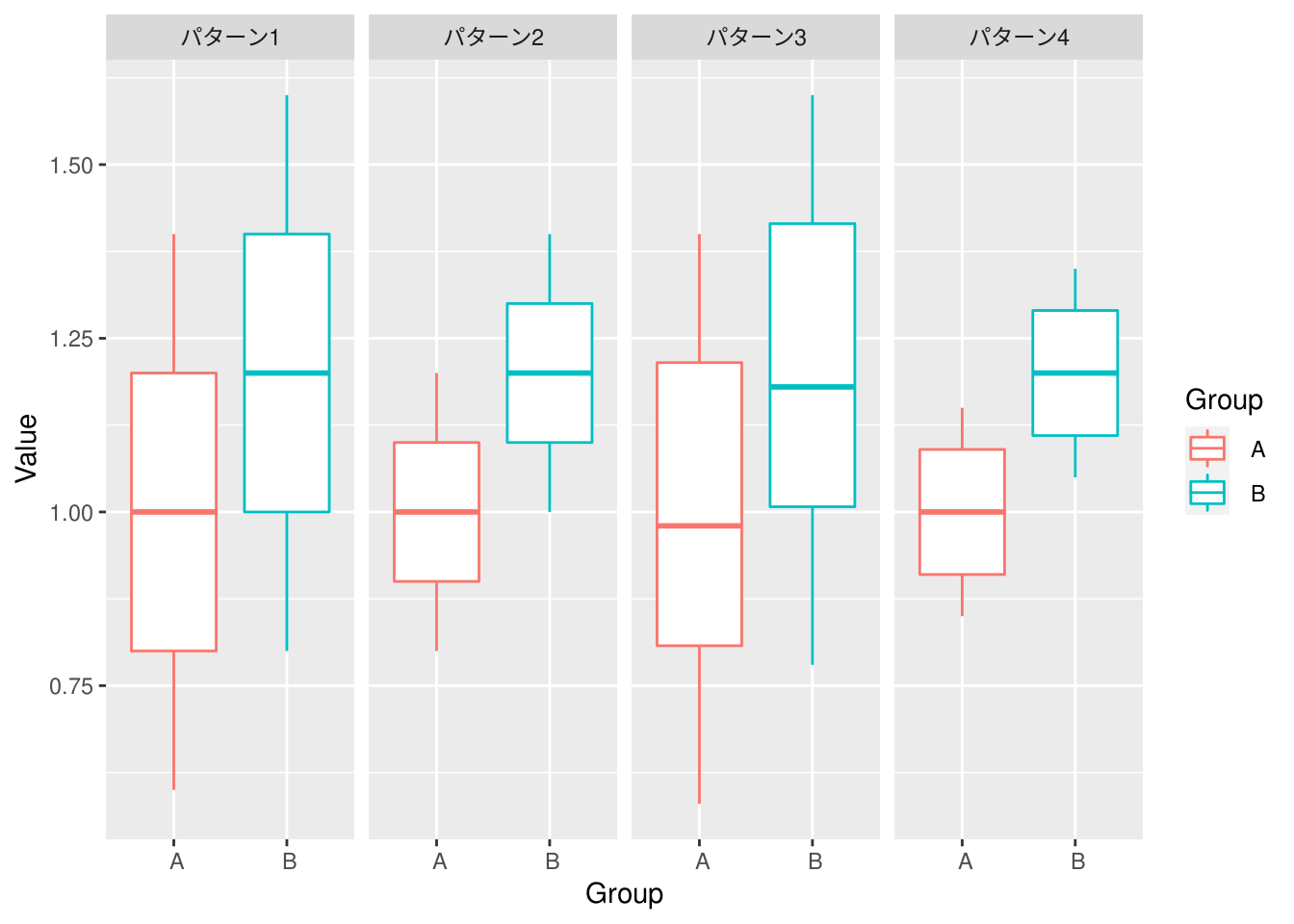
- パターン1とパターン2は
- データ数は等しい
- パターン2の方が標準偏差が小さい（分離性が高い）
\[\mbox{パターン2} < \mbox{パターン1}\]
- パターン2とパターン4は
- 標準偏差は等しい
- パターン4の方がデータ数が少ない（半分以下）
\[\mbox{パターン2} < \mbox{パターン4}\]
- パターン2とパターン3は
- パターン2の方が標準偏差が小さい（約半分）
- パターン3の方がデータ数が多い（倍）
\[\mbox{パターン2} < \mbox{パターン3}\]
- パターン3とパターン4は
- 標準偏差は同じ
- パターン4の方がデータ数が少ない（半分以下）
\[\mbox{パターン3} < \mbox{パターン4}\]
- パターン1とパターン4は
- パターン1の方がデータ数が多い（倍以上）
- パターン4の方が標準偏差が小さい（約半分）
\[\mbox{パターン4} < \mbox{パターン1}\]
したがって、4パターンのp値の関係は以下と推測できる。
\[\mbox{パターン2} < \mbox{パターン3} < \mbox{パターン4} < \mbox{パターン1}\]
Q2 t検定のp値で結果を確認する（演習3）
Rで二群の平均値の差の検定を行うにはt.test()関数を用います。
パターン1のt検定結果
Two Sample t-test
data: Value by Group
t = -1.5492, df = 16, p-value = 0.1409
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
-0.4736786 0.0736786
sample estimates:
mean in group A mean in group B
1.0 1.2 パターン2のt検定結果
Two Sample t-test
data: Value by Group
t = -3.0984, df = 16, p-value = 0.006903
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
-0.3368393 -0.0631607
sample estimates:
mean in group A mean in group B
1.0 1.2 パターン3のt検定結果
Two Sample t-test
data: Value by Group
t = -2.26, df = 34, p-value = 0.03034
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
-0.37984565 -0.02015435
sample estimates:
mean in group A mean in group B
1.003889 1.203889 パターン4のt検定結果
Two Sample t-test
data: Value by Group
t = -2.0927, df = 6, p-value = 0.08129
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
-0.43384763 0.03384763
sample estimates:
mean in group A mean in group B
1.0 1.2 t検定結果の比較（p値順）
"./data/Pre_P52_4パターン.csv" %>%
read.csv() %>%
dplyr::group_by(Pattern) %>%
tidyr::nest() %>%
dplyr::mutate(out = purrr::map(.x = data,
.f = ~ with(.x, t.test(Value ~ Group,
var.equal = TRUE) %>%
broom::tidy()))) %>%
tidyr::unnest(out) %>%
dplyr::select(Pattern, p.value, t.value = statistic) %>%
dplyr::arrange(p.value) %>%
dplyr::left_join(x, by = c("Pattern" = "パターン")) %>%
df_print()
個人演習（ツール導入すべきか？）
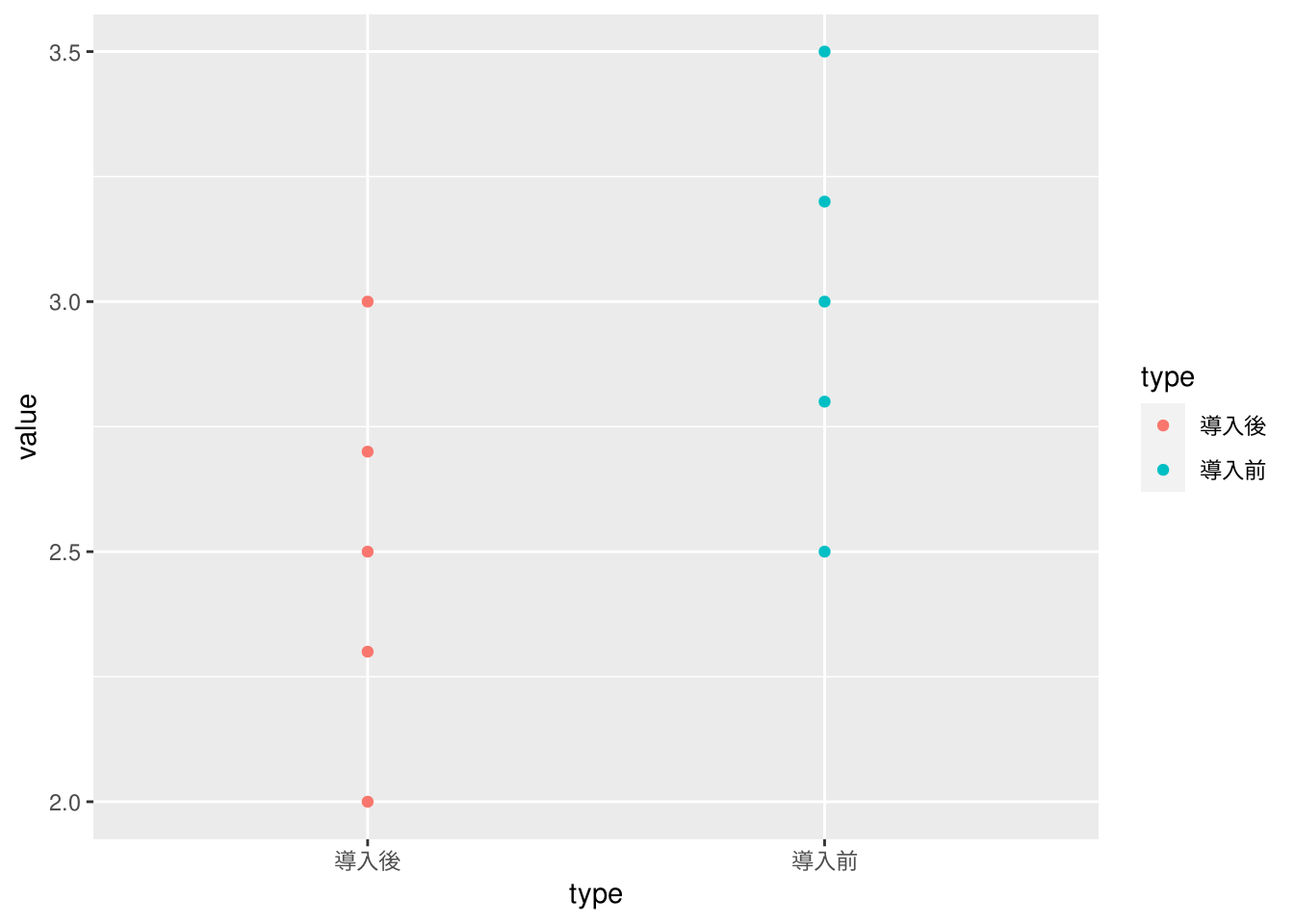
ツール導入前後の欠陥密度データです。データ間に対応はありません。
ツール導入前後の欠陥密度
"./data/Pre_P13_ツールを導入すべきか.csv" %>%
read.csv() %>%
df_print()
欠陥密度の平均値の差は\(0.5\)なので約\(17\%\)改善していることになります。
ツール導入前後の欠陥密度の平均値
"./data/Pre_P13_ツールを導入すべきか.csv" %>%
read.csv() %>%
dplyr::summarise(dplyr::across(dplyr::everything(), mean)) %>%
df_print()
Q1 t検定で検証する （演習4）
ツール導入前後の欠陥密度に優位な差があるかをt検定で検証します。なお、両者のデータは等分散であると仮定、有意水準は\(5\%\)とします。
欠陥密度の平均値の差の検定
Two Sample t-test
data: 導入前 and 導入後
t = 2.0761, df = 8, p-value = 0.07154
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.05535934 1.05535934
sample estimates:
mean of x mean of y
3.0 2.5 p値が有意水準を下回らないので、帰無仮説は棄却できず有意な差がある（二群の平均値の差が\(0\)でない）とは言えない。したがって、このデータからはツール導入の効果は見込めない。ただし、p値からみてデータ数を増やして再検定すれば有意になる可能性があるかも知れない。
参考）欠陥密度の分布
"./data/Pre_P13_ツールを導入すべきか.csv" %>%
read.csv() %>%
tidyr::pivot_longer(cols = dplyr::everything(),
names_to = "type", values_to = "value") %>%
ggplot2::ggplot(ggplot2::aes(x = type, y = value, colour = type)) +
ggplot2::geom_jitter(position = "dodge")Warning: Width not defined. Set with `position_dodge(width = ?)`