Rで学ぶ『完全独習統計学入門』 - 1 度数分布表とヒストグラムでデータの特徴を浮き彫りにする

1.1 生データでは何もわからないから統計を使う

　テキストP16の図表1-1のデータは4列20行からなるデータです。

　
　Rでは、このような形式のデータ（雑然データ）をそのまま使わずに整然データ（Tidy Data）と呼ばれる形式に変換した方が効率的に処理できます。変換にはtidyverseファミリーを利用するのが効率的です。

Tidy Dataへの変形

library(tidyverse)  # load tidyverse package

x <- "./data/P16_図表1-1 .csv" %>% 
  readr::read_csv(col_names = FALSE, show_col_types = FALSE) %>% 
  tidyr::pivot_longer(cols = dplyr::starts_with("X"),
                      names_to = "name", values_to = "value") %>% 
  dplyr::arrange(name) %>% 
  dplyr::select(height = value)

x %>% 
  df_print()

　このような形式（Tidy Data）に変換することで、様々な統計量を効率的に求めることができるようになります。

1.2 ヒストグラムを作る

　テキストでは度数分布表を作成してからヒストグラムを描いています。その手順は

最大・最小値を求める
階級を決める
度数をカウントする
相対度数を求める
累積度数を求める
- ここまでが度数分布表の作成
度数分布表をもとにヒストグラムを描く

となっていますが、Rではhist()関数だけでヒストグラムを描くことができます。hist()関数の引数はベクトル型に限定されますので、データフレーム型の場合は参照演算子（$）などでベクトル型データを取り出す必要があります。

R標準のヒストグラム関数

hist(x = x$height)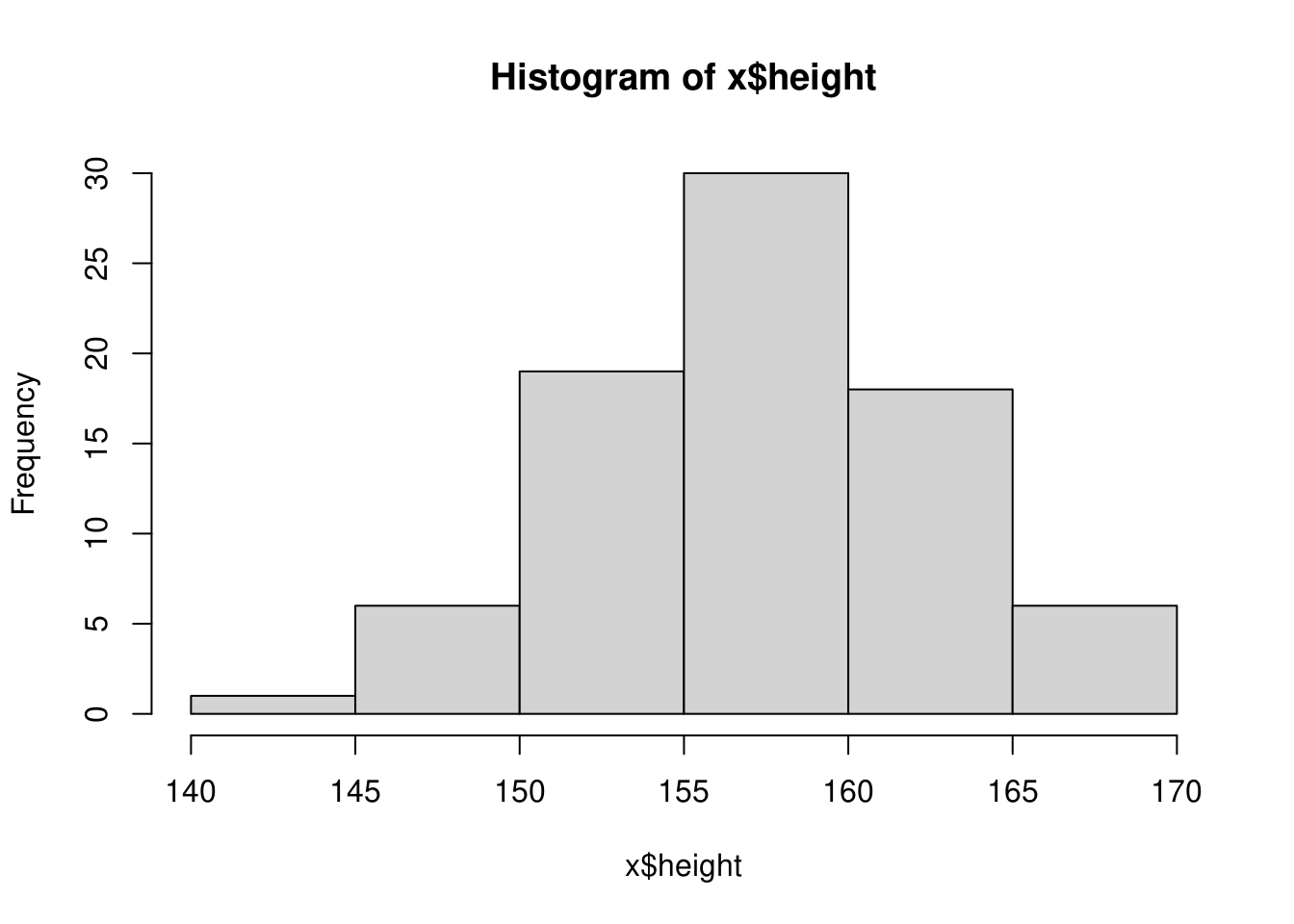

　
　hist()関数はヒストグラムを描くために必要となる階級や度数、階級値などの情報を出力することも可能です。

階級などを表示させる方法

hist(x = x$height, plot = FALSE)

$breaks
[1] 140 145 150 155 160 165 170

$counts
[1]  1  6 19 30 18  6

$density
[1] 0.0025 0.0150 0.0475 0.0750 0.0450 0.0150

$mids
[1] 142.5 147.5 152.5 157.5 162.5 167.5

$xname
[1] "x$height"

$equidist
[1] TRUE

attr(,"class")
[1] "histogram"

主な出力の意味
出力名	意味	備考
`$breaks`	階級	デフォルトはスタージェスの公式^*後述にもとづく区切り（幅）
`$counts`	度数	各階級に入るデータの個数
`$density`	密度	密度推定値
`$mids`	階級値	階級の中央値（階級の単純平均）

　表形式の度数分布表を作成する場合は以下のようにコード処理します。

度数分布表の作成

x %>% 
  # 階級を求めて、データを階級ごとに分ける
  dplyr::mutate(class = cut(height,
                            breaks = pretty(height, n = nclass.Sturges(height)),
                            include.lowest = FALSE, right = TRUE)) %>% 
  # 階級ごとの度数を求める
  dplyr::count(class) %>% 
  # 累積度数、相対度数、累積相対度数を求める
  dplyr::mutate(cumsum_n = cumsum(n),
                prop = prop.table(n), cumsum_prop = cumsum(prop)) %>% 
  # 階級値を求める
  dplyr::mutate(class_value = as.character(class)) %>%
  tidyr::separate(class_value, into = c("l", "h"), sep = ",") %>% 
  dplyr::mutate(l = as.integer(stringr::str_remove(l, "[[:punct:]]")) + 1L,
                h = as.integer(stringr::str_remove(h, "[[:punct:]]")),
                mids = (l + h) / 2L) %>%
  # 変数名を日本語にする
  dplyr::select(`階級` = class, `階級値` = mids,
                `度数` = n, `累積度数` = cumsum_n,
                `相対度数` = prop, `累積相対度数` = cumsum_prop) %>% 
  df_print()

　
　以降の項は度数分布表の作成に必要な関数の使い方を紹介していますので、不要な方は演習問題まで読み飛ばしてください。

1.2.1 階級を求める

以降に出てくるwith()関数は、第一引数で指定するデータフレーム型変数内の変数名を第二引数内で参照演算子（$）を用いることなく参照できるようにする関数です。

　階級を求めるにはpretty()関数を使います。

階級を求める

with(x, pretty(x = height,
               n = nclass.Sturges(height)))

[1] 140 145 150 155 160 165 170

　第一引数xには階級を求めたいベクトル型データを第二引数nには階級を区切りたい数（階級数）を指定します。ここでは、階級数nにはスタージェスの公式から求めた階級数を指定しています。
　ただし、xで指定したデータが階級に収まるように適切な丸め処理を行いますので、指定した階級数とは異なる階級が求められることもあります。

　スタージェスの公式は、階級数を$k$、データのサイズ（数）を$n$とした場合、下式で定義されます。

\[k = \lceil \log_2n + 1 \rceil\]

　スタージェスの公式はnclass.Sturgess()関数として実装されています。

スタージェスの公式に基づく階級数

with(x, nclass.Sturges(height))

[1] 8

　
　スタージェスの公式はヒストグラムを平滑化し過ぎる傾向があると言われています。気になる場合はスコットの選択（nclass.scott()）やフリードマン=ダイアコニスの選択（nclass.FD()）を試して見てください。

1.2.2 データを各階級に分類する

参考）身長データ（元データ）

with(x, height)

 [1] 151 154 160 160 163 156 158 156 154 160 154 162 156 162 157 162 162 169 150
[20] 162 152 161 159 164 168 153 160 155 160 158 160 150 163 155 157 162 154 161
[39] 153 154 151 155 158 146 149 165 169 154 155 166 165 161 148 143 156 162 158
[58] 156 159 164 167 159 157 151 159 156 151 160 153 156 146 166 151 159 157 156
[77] 162 156 156 161

　
　データを階級分けするにはcut()関数を使います。

データの階級分け

with(x, cut(x = height,
            breaks = pretty(height,
                            n = nclass.Sturges(height))))

 [1] (150,155] (150,155] (155,160] (155,160] (160,165] (155,160] (155,160]
 [8] (155,160] (150,155] (155,160] (150,155] (160,165] (155,160] (160,165]
[15] (155,160] (160,165] (160,165] (165,170] (145,150] (160,165] (150,155]
[22] (160,165] (155,160] (160,165] (165,170] (150,155] (155,160] (150,155]
[29] (155,160] (155,160] (155,160] (145,150] (160,165] (150,155] (155,160]
[36] (160,165] (150,155] (160,165] (150,155] (150,155] (150,155] (150,155]
[43] (155,160] (145,150] (145,150] (160,165] (165,170] (150,155] (150,155]
[50] (165,170] (160,165] (160,165] (145,150] (140,145] (155,160] (160,165]
[57] (155,160] (155,160] (155,160] (160,165] (165,170] (155,160] (155,160]
[64] (150,155] (155,160] (155,160] (150,155] (155,160] (150,155] (155,160]
[71] (145,150] (165,170] (150,155] (155,160] (155,160] (155,160] (160,165]
[78] (155,160] (155,160] (160,165]
Levels: (140,145] (145,150] (150,155] (155,160] (160,165] (165,170]

　
　cut()関数の第一引数xには階級分けの対象となるベクトル型変数を第二引数breaksには前項で求めた階級を指定します。breaks引数には任意の階級、例えばbreaks = c(140, 155, 170)のような指定も可能です。

階級の境界値はどちらに含まれるのか？

　cut()関数の出力は、(140,145] (145,150]のように階級間で同じ値（この場合は145）が含まれます。では、145はどちらの階級に含まれるのでしょうか？答えは、添えられている括弧にあります。

(140,145]

は「140を超えて145以下」となりますので、次の

(145,150]

は同様に「145を超えて150以下」となります。階級間の境界値である145は(140, 145]側に入ります。

(は「超えて」（境界値を含まない）、]は「以下」（境界値を含む）

で、逆向きの場合は

)は「未満」（境界値を含まない）、[は「以上」（境界値を含む）

となります。hist()関数の階級も同様です。

　境界値をどちらに含めるかはinclude.lowest引数とright引数で指定できます。

option	`right = TRUE`	`right = FALSE`
`include.lowest = TRUE`	`[l,u] ... (l,u]`	`[l,u) ... [l,u]`
`include.lowest = FALSE`	`(l,u] ... (l,u]`^*	`[l,u) ... [l,u)`

　^*デフォルト

　例えばデータの最大値と最小値を境界値として含む階級を指定した場合、include.lowest = FALSE, right = FALSEと指定すると最大値が階級に含まれなくなる場合があります。

以上、未満の場合

with(x, cut(height, breaks = c(143, 155, 169),
            include.lowest = FALSE, right = FALSE))

 [1] [143,155) [143,155) [155,169) [155,169) [155,169) [155,169) [155,169)
 [8] [155,169) [143,155) [155,169) [143,155) [155,169) [155,169) [155,169)
[15] [155,169) [155,169) [155,169) <NA>      [143,155) [155,169) [143,155)
[22] [155,169) [155,169) [155,169) [155,169) [143,155) [155,169) [155,169)
[29] [155,169) [155,169) [155,169) [143,155) [155,169) [155,169) [155,169)
[36] [155,169) [143,155) [155,169) [143,155) [143,155) [143,155) [155,169)
[43] [155,169) [143,155) [143,155) [155,169) <NA>      [143,155) [155,169)
[50] [155,169) [155,169) [155,169) [143,155) [143,155) [155,169) [155,169)
[57] [155,169) [155,169) [155,169) [155,169) [155,169) [155,169) [155,169)
[64] [143,155) [155,169) [155,169) [143,155) [155,169) [143,155) [155,169)
[71] [143,155) [155,169) [143,155) [155,169) [155,169) [155,169) [155,169)
[78] [155,169) [155,169) [155,169)
Levels: [143,155) [155,169)

　
　逆にinclude.lowest = FALSE, right = TRUEと指定すると最小値が階級が階級に含まれなくなる場合があります。

超えて、以下の場合

with(x, cut(height, breaks = c(143, 155, 169),
            include.lowest = FALSE, right = TRUE))

 [1] (143,155] (143,155] (155,169] (155,169] (155,169] (155,169] (155,169]
 [8] (155,169] (143,155] (155,169] (143,155] (155,169] (155,169] (155,169]
[15] (155,169] (155,169] (155,169] (155,169] (143,155] (155,169] (143,155]
[22] (155,169] (155,169] (155,169] (155,169] (143,155] (155,169] (143,155]
[29] (155,169] (155,169] (155,169] (143,155] (155,169] (143,155] (155,169]
[36] (155,169] (143,155] (155,169] (143,155] (143,155] (143,155] (143,155]
[43] (155,169] (143,155] (143,155] (155,169] (155,169] (143,155] (143,155]
[50] (155,169] (155,169] (155,169] (143,155] <NA>      (155,169] (155,169]
[57] (155,169] (155,169] (155,169] (155,169] (155,169] (155,169] (155,169]
[64] (143,155] (155,169] (155,169] (143,155] (155,169] (143,155] (155,169]
[71] (143,155] (155,169] (143,155] (155,169] (155,169] (155,169] (155,169]
[78] (155,169] (155,169] (155,169]
Levels: (143,155] (155,169]

1.2.3 度数を求める

　度数を求めるには各階級の数を数えます。数を数えるにはtable()関数やdplyr::count()関数を使います。table()関数はベクトル型を対象として、dplyr::count()関数はデータフレーム型を対象として個数をカウントする関数です。

度数のカウント

with(x, table(cut(height,
                  breaks = pretty(height,
                                  n = nclass.Sturges(height)))))


(140,145] (145,150] (150,155] (155,160] (160,165] (165,170] 
        1         6        19        30        18         6

度数のカウント（データフレームの場合）

x %>% 
  dplyr::mutate(class = cut(height,
                            breaks = pretty(height,
                                            n = nclass.Sturges(height)))) %>% 
  dplyr::count(class) %>% 
  df_print()

1.2.4 累積度数、相対度数、累積相対度数を求める

　累積度数（度数の累積和）を求めるにはcumsum()関数を使います。

累積度数を求める

with(x, cumsum(table(cut(height,
                         breaks = pretty(height,
                                         n = nclass.Sturges(height))))))

(140,145] (145,150] (150,155] (155,160] (160,165] (165,170] 
        1         7        26        56        74        80

　
　相対度数を求めるにはprop.table()関数を使います。

相対度数を求める

with(x, prop.table(table(cut(height,
                             breaks = pretty(height,
                                             n = nclass.Sturges(height))))))


(140,145] (145,150] (150,155] (155,160] (160,165] (165,170] 
   0.0125    0.0750    0.2375    0.3750    0.2250    0.0750

　累積相対度数は相対度数の累積和ですので、prop.table()関数の結果をcumsum()関数に渡すことで求めることができます。

累積相対度数を求める

with(x, cumsum(prop.table(
  table(cut(height,
            breaks = pretty(height,
                            n = nclass.Sturges(height)))))))

(140,145] (145,150] (150,155] (155,160] (160,165] (165,170] 
   0.0125    0.0875    0.3250    0.7000    0.9250    1.0000

1.2.5 階級値を求める

　階級値は階級の文字列から下端と上端の境界値を抜き出し、下式で単純平均として求めています。

\[\frac{(\mbox{下端} + 1) + \mbox{上端}}{2}\]

　手順としては以下のようになります。

as.character()関数で階級（class）を文字型に変換し、新しい変数（class_value）を作成する
tidyr::separate()関数で文字型の変数（class_value）を,の前後で二つの変数（l, h）に分割する
stringr::str_remove関数で二つの変数（l, h）から(や]を取り除きas.numeric()関数で文字列から数値に変換する
数値に変換された二つの変数から（l, h）平均値を求める

階級値を求める

x %>% 
  # 階級を求めて、データを階級ごとに分ける
  dplyr::mutate(class = cut(height,
                            breaks = pretty(height,
                                            n = nclass.Sturges(height)),
                            include.lowest = FALSE,
                            right = TRUE)) %>% 
  # 階級ごとの度数を求める
  dplyr::count(class) %>% 
  # 階級値を求める
  dplyr::mutate(class_value = as.character(class)) %>% 
  tidyr::separate(class_value, into = c("l", "h"), sep = ",") %>% 
  dplyr::mutate(l = as.numeric(stringr::str_remove(l, "[[:punct:]]")),
                h = as.numeric(stringr::str_remove(h, "[[:punct:]]"))) %>% 
  dplyr::mutate(mids = ((l + 1) + h) / 2) %>% 
  df_print()

1.3 練習問題

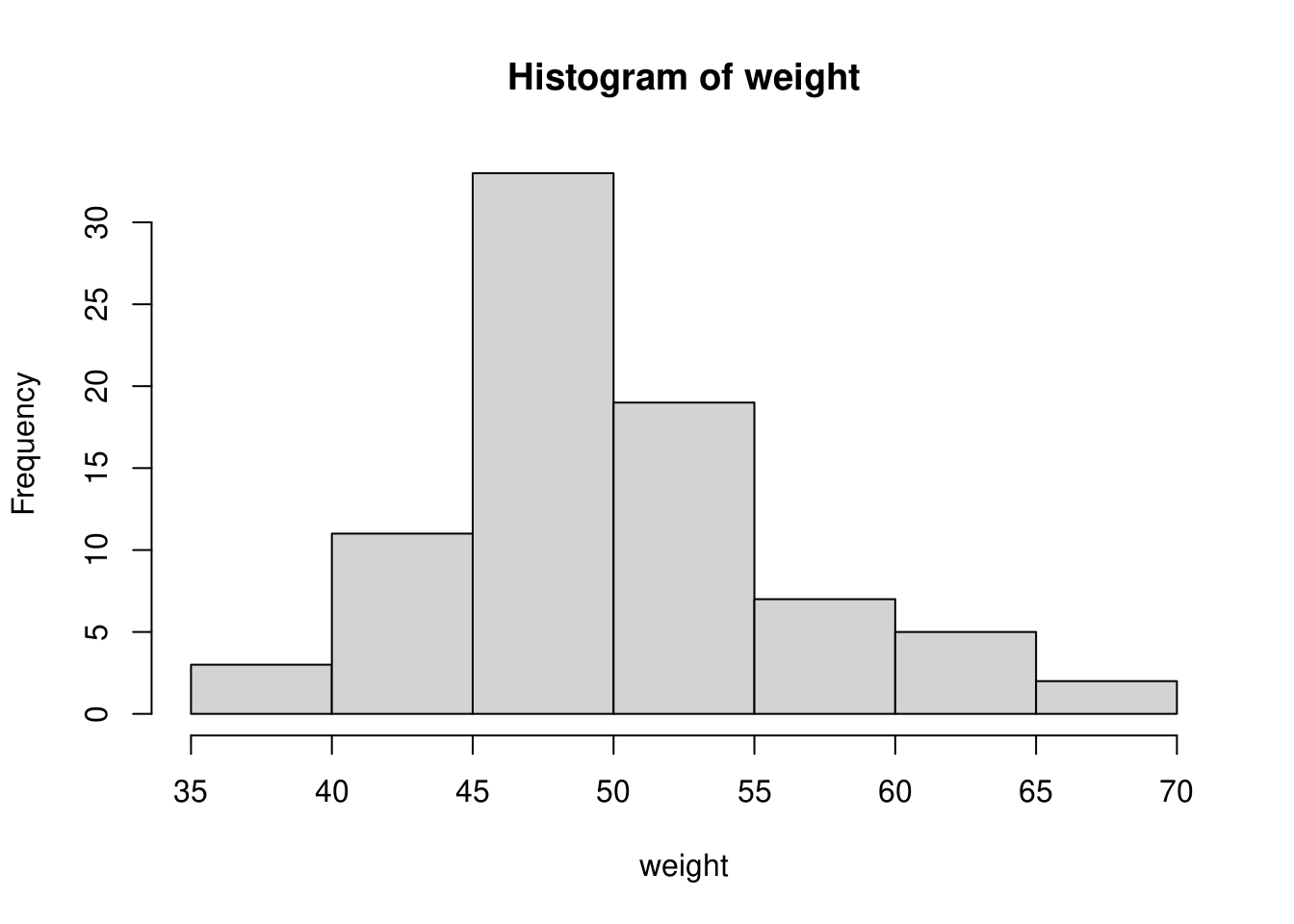
　テキストP23にあるデータで度数分布表とヒストグラムを作成する。

解答例

　まず、処理しやすいように下記のように対象データを変形しdfというデータフレーム型の変数に格納しておきます。

整形済の処理対象データ（体重データ）

df %>% 
  df_print()

　度数分布表を身長の場合と同じ要領で作成します。

度数分布表の作成

df %>% 
  dplyr::mutate(class = cut(weight,
                            breaks = pretty(weight,
                                            n = nclass.Sturges(weight)),
                            include.lowest = FALSE,
                            right = TRUE)) %>% 
  # 階級ごとの度数を求める
  dplyr::count(class) %>% 
  # 累積度数、相対度数、累積相対度数を求める
  dplyr::mutate(cumsum_n = cumsum(n),
                prop = prop.table(n),
                cumsum_prop = cumsum(prop)) %>% 
  # 階級値を求める
  dplyr::mutate(class_value = as.character(class)) %>%
  tidyr::separate(class_value, into = c("l", "h"), sep = ",") %>% 
  dplyr::mutate(l = as.integer(stringr::str_remove(l, "[[:punct:]]")) + 1L,
                h = as.integer(stringr::str_remove(h, "[[:punct:]]")),
                mids = (l + h) / 2L) %>%
  # 変数名を日本語にする
  dplyr::select(`階級` = class, `階級値` = mids,
                `度数` = n, `累積度数` = cumsum_n,
                `相対度数` = prop,
                `累積相対度数` = cumsum_prop) %>% 
  df_print()

　ヒストグラムを描きます。

ヒストグラムを描く

with(df, hist(weight))

　
以上

ヒストグラムを描くポイント

　ヒストグラムを描く（度数分布表を作成する）際のポイントは下記の点です。

階級の決め方
階級の境界の扱い

階級の決め方

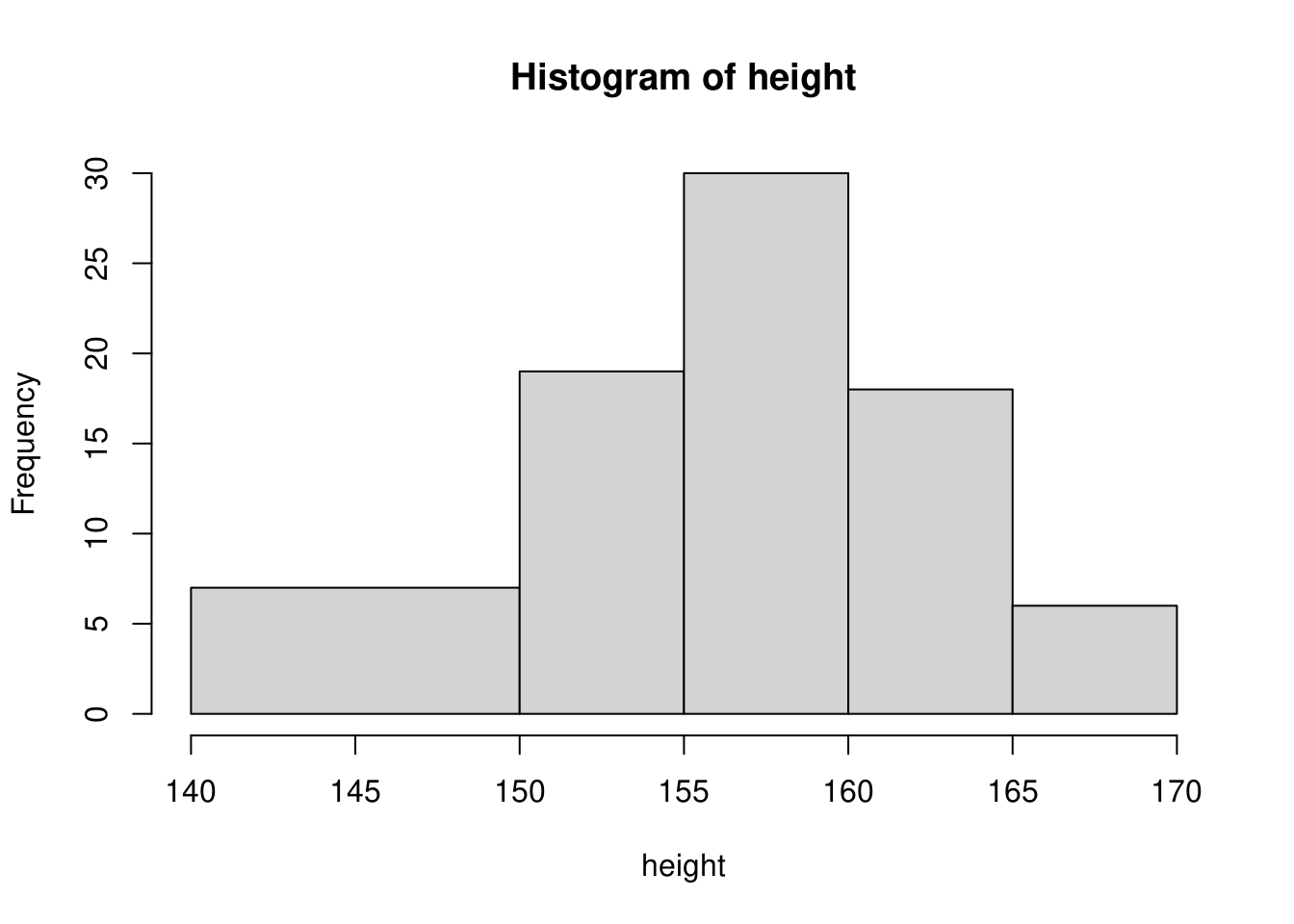
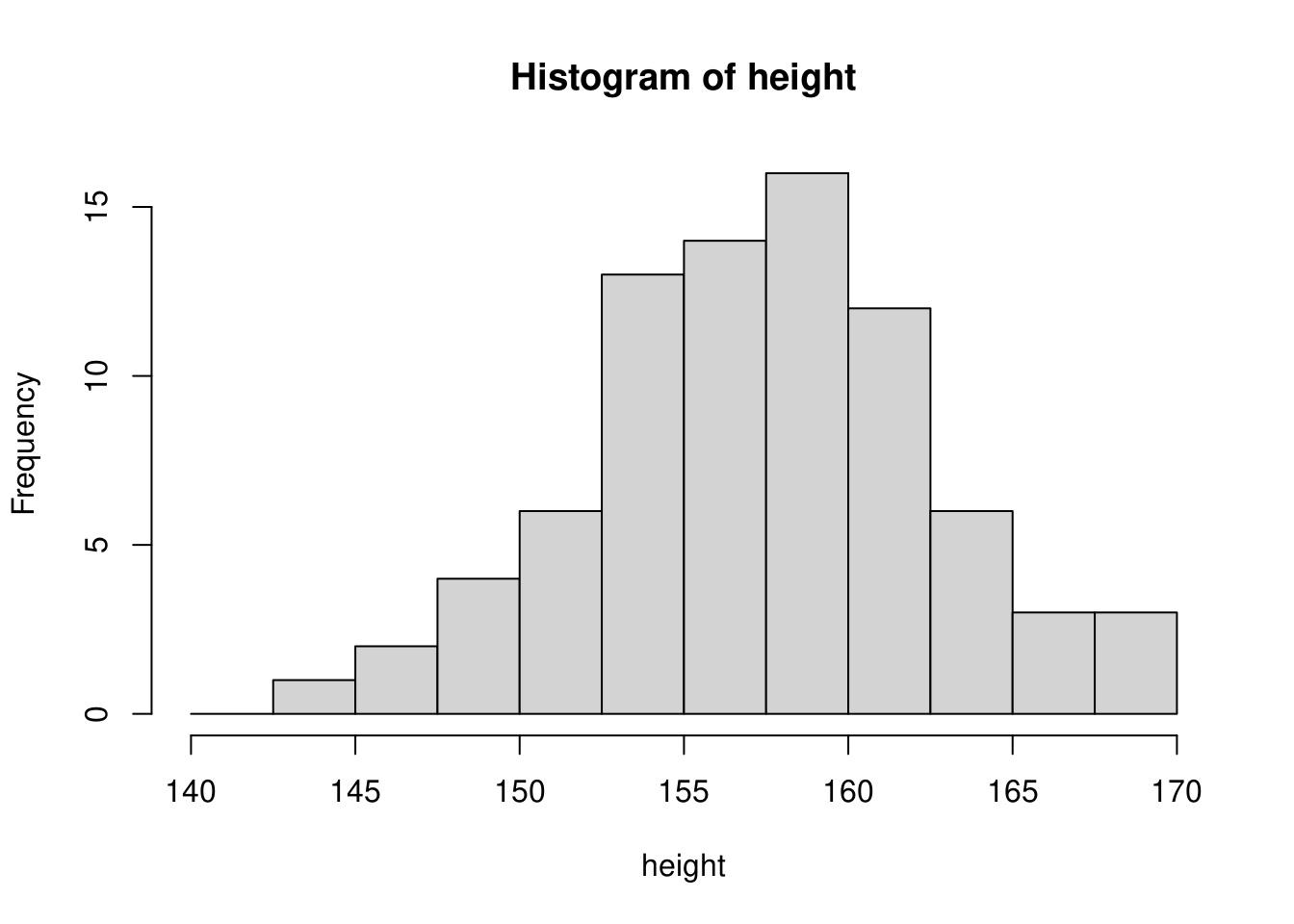
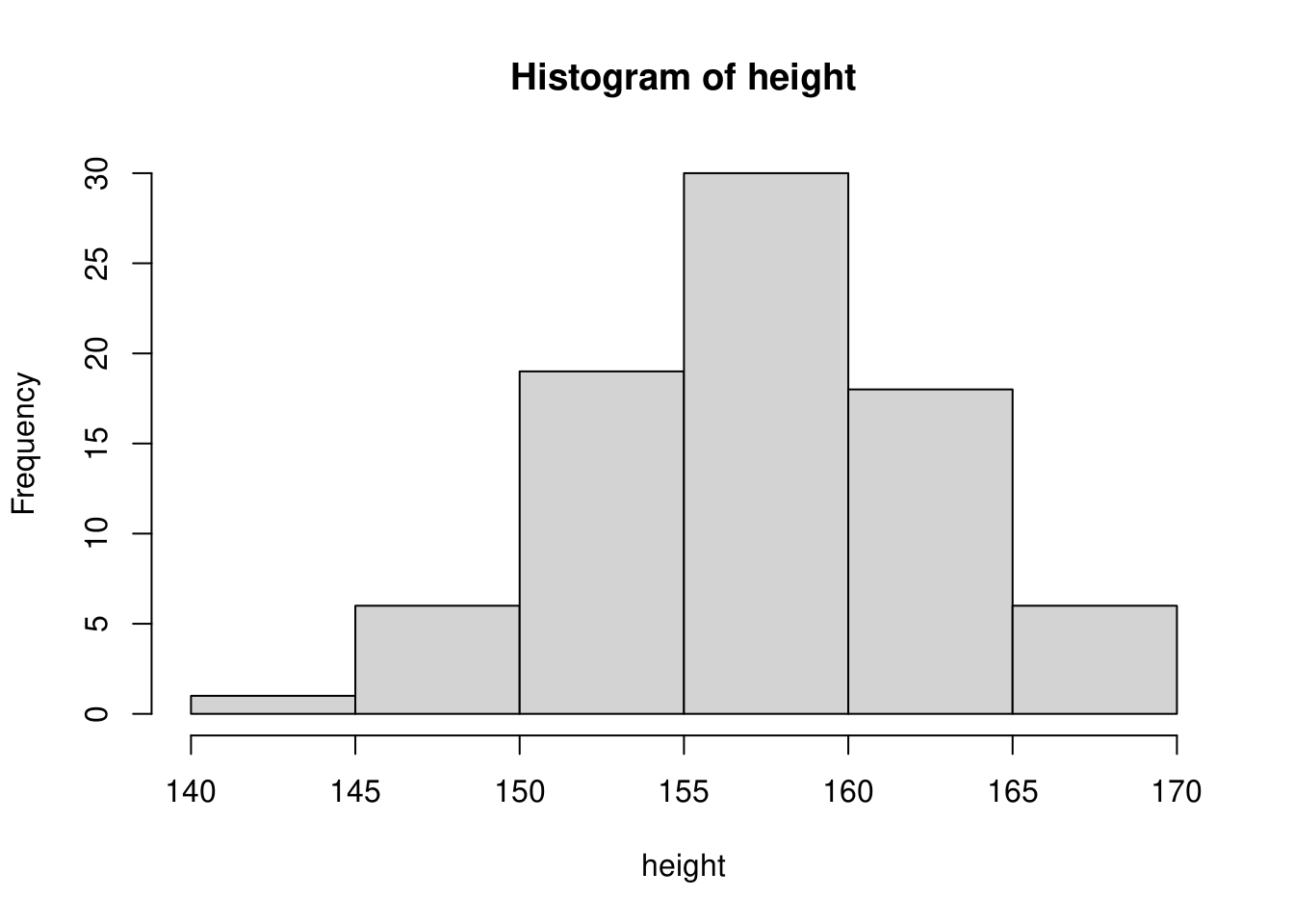
　階級を決める方法は特に定められていません。データが取る幅を見て切のよい値にすることが多いようです。ただし、階級のとり方によりヒストグラムの形状が変わる点には注意が必要です。例えば、身長データに対する階級をテキストと同様に$5cm$幅とした場合は下図のような形状になります。

階級幅5cmの場合のヒストグラム

with(x, hist(height,
             breaks = seq(from = 140, to = 170, by = 5)))

　
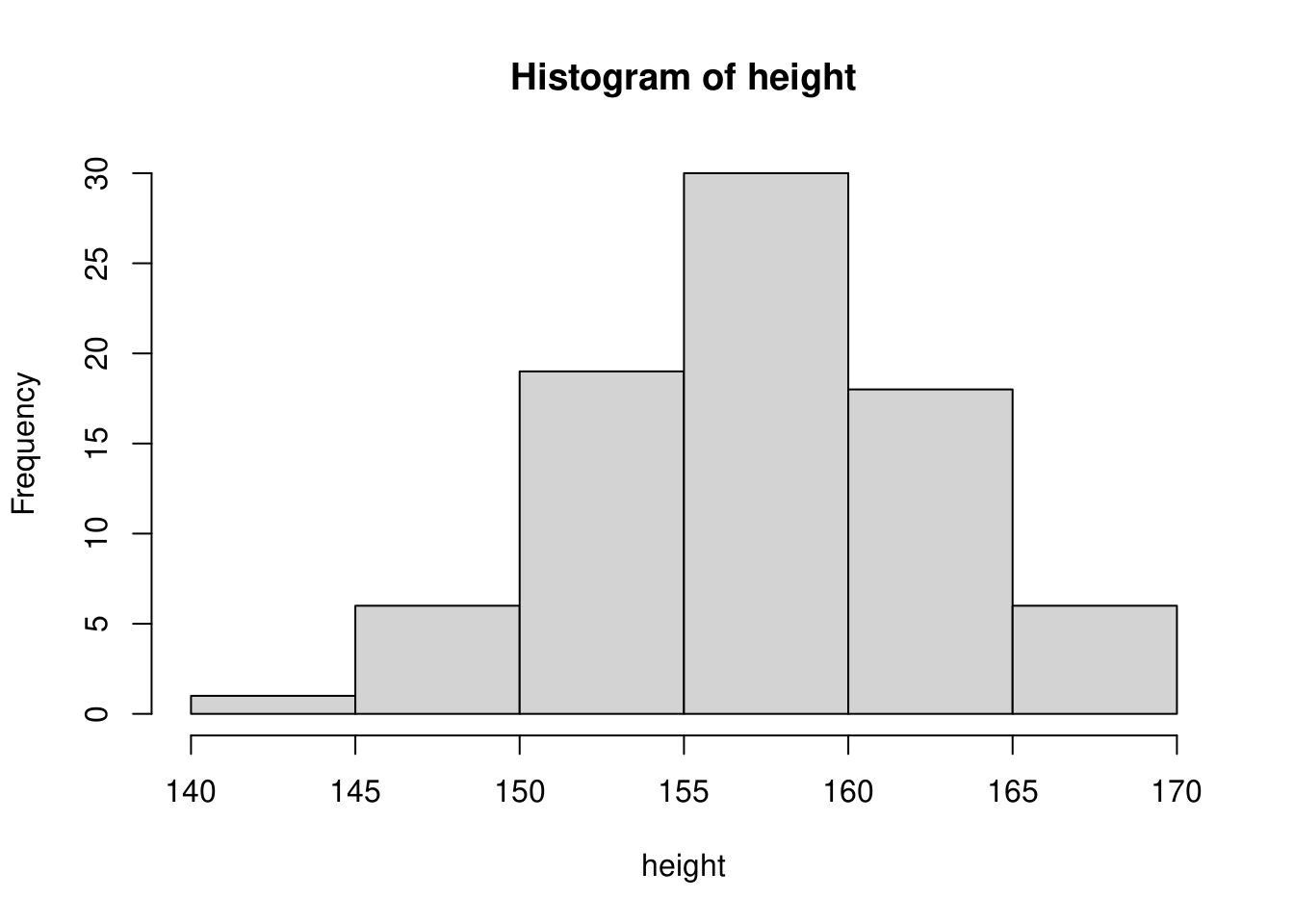
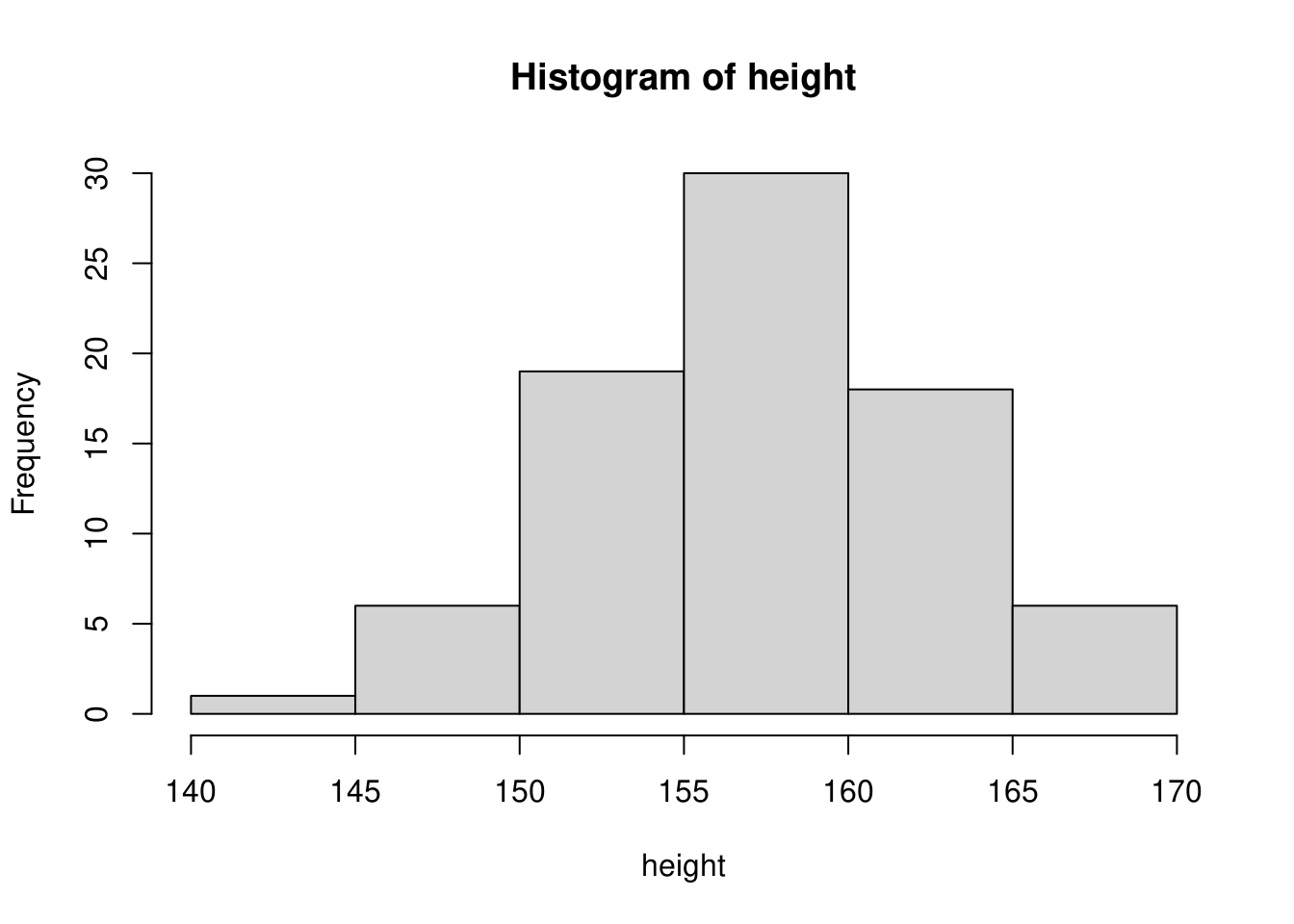
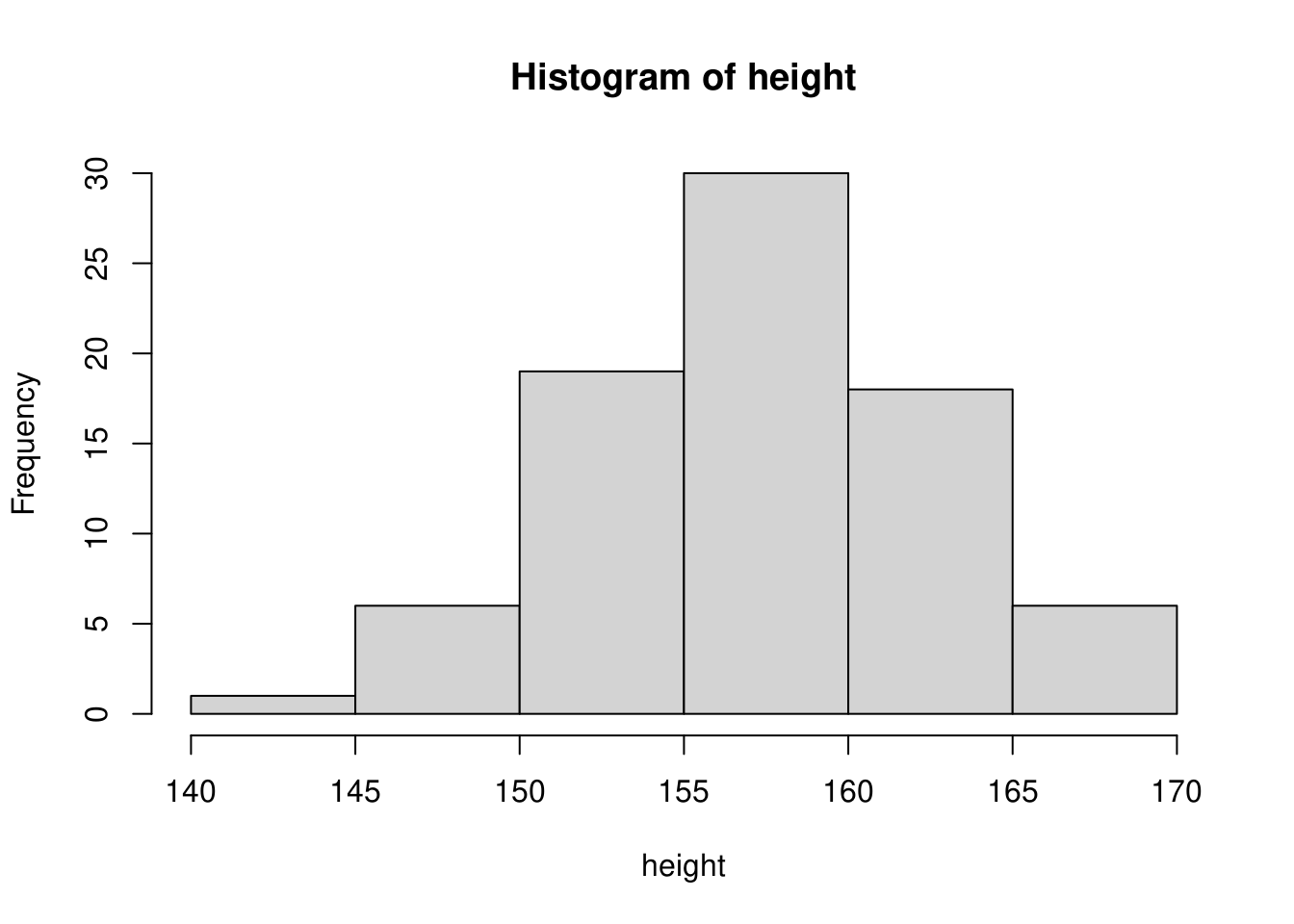
　階級を倍の$10cm$幅とすると下図のようになります。

階級幅10cmの場合のヒストグラム

with(x, hist(height,
             breaks = seq(from = 140, to = 170, by = 10)))

　
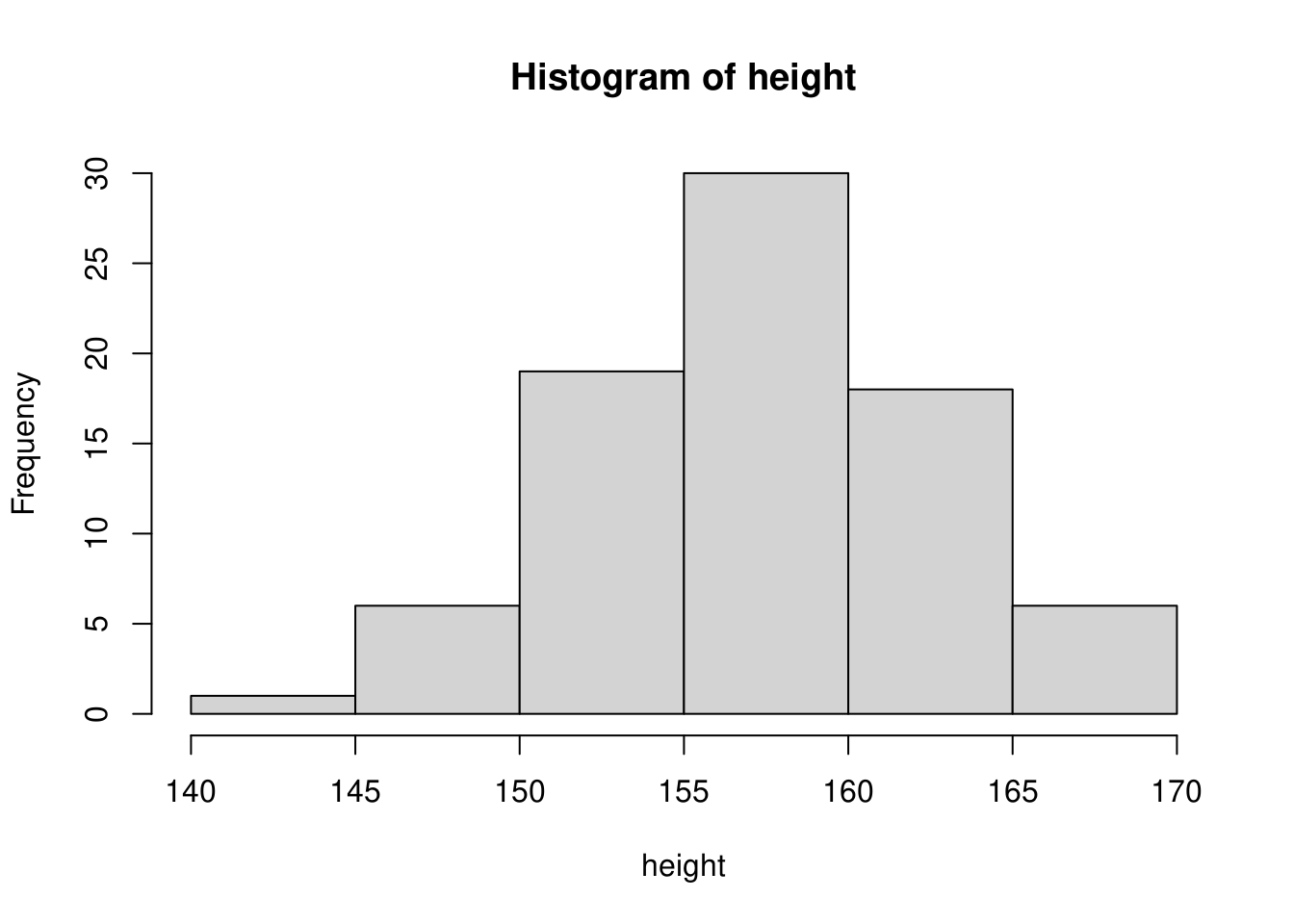
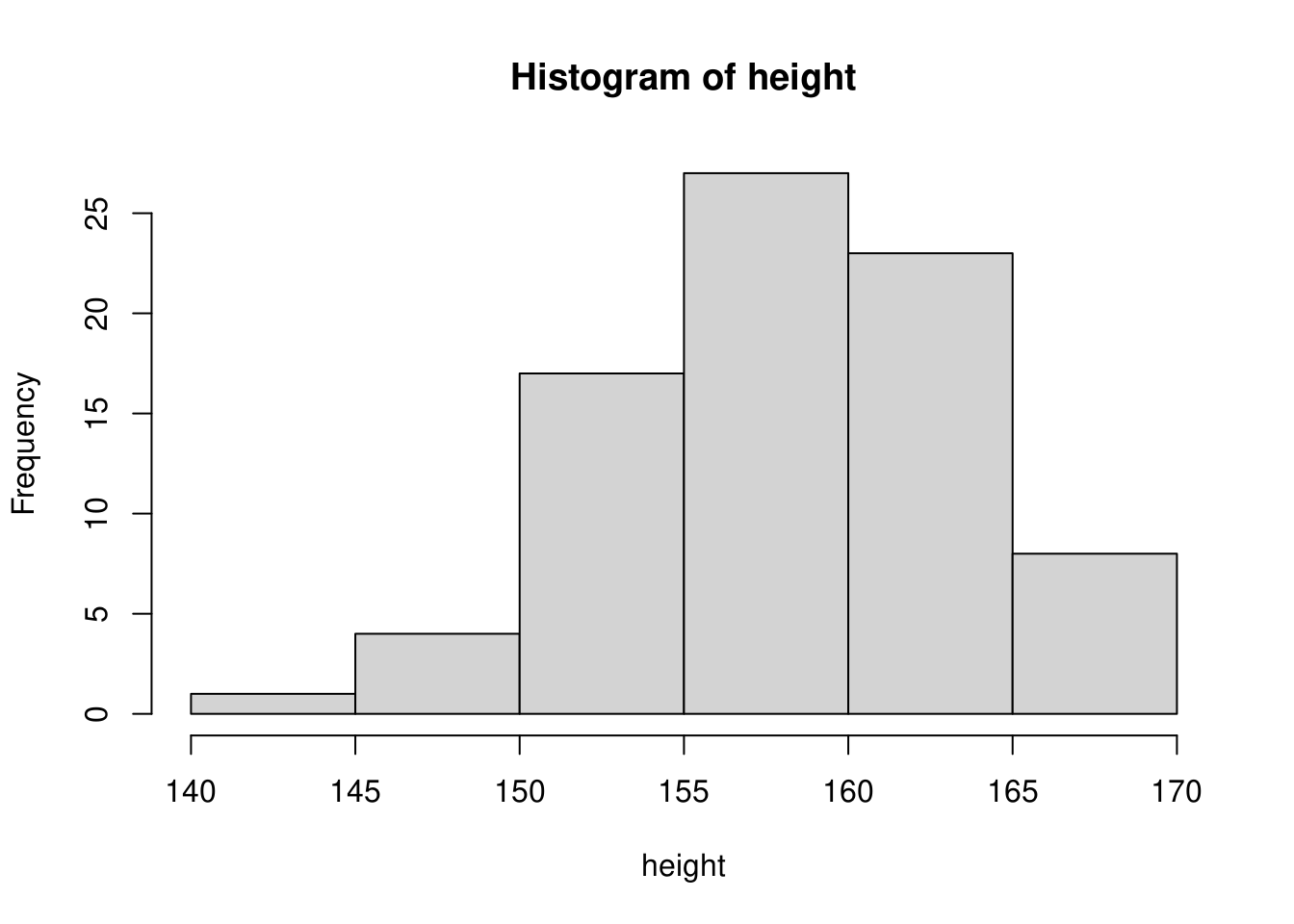
　逆に階級を半分の$2.5cm$幅とすると下図のようになります。

階級幅2.5cmの場合のヒストグラム

with(x, hist(height,
             breaks = seq(from = 140, to = 170, by = 2.5)))

　
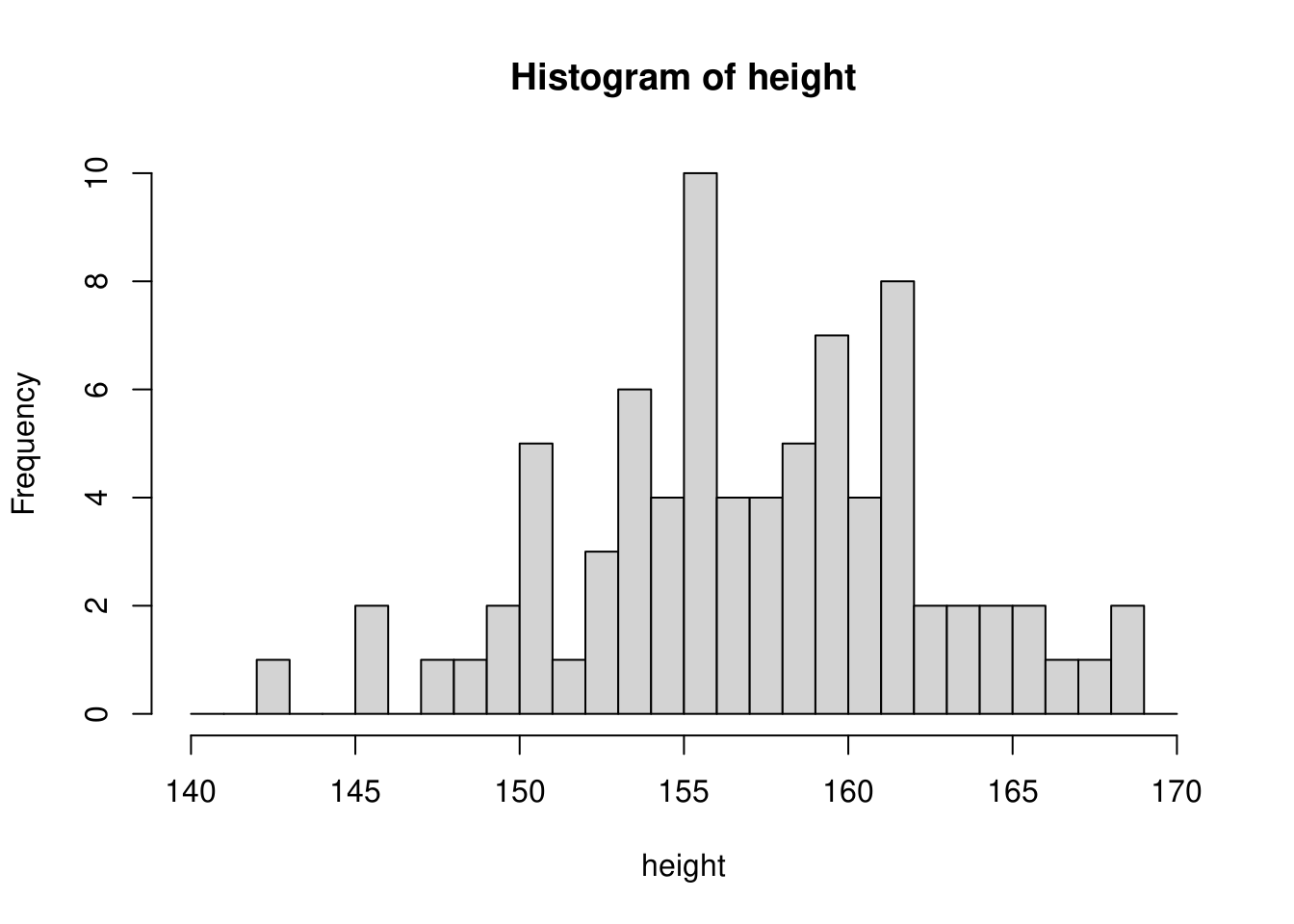
　更に細かくして$1cm$幅にすると下図のように歯抜けがある形状になります。

階級幅1cmの場合のヒストグラム

with(x, hist(height,
             breaks = seq(from = 140, to = 170, by = 1.0)))

　
　このように階級の決め方次第でヒストグラムの形状が変わってくることが分かります。ヒストグラムはデータの分布をみるために使うグラフですので、過大な階級幅や過小な階級幅で描くことは好ましくありませんので、適切な値を選ぶようにしてください。

計算で階級を決める

　適切な階級をどのように決めれば良いか迷う場合には、下表のような計算方法が提案されていますのでこれらを試してみてください。

階級の求め方	階級数（$k$）・階級幅（$h$）	備考
平方根選択（Square-root choice）	$k = \sqrt{n}$
スタージェスの公式（Sturges’s formula）	$k = \lceil \log_2n + 1 \rceil$	$n \geq 30$が前提
スコットの選択（Scott’s choice）	$h = \frac{3.5\sigma}{n^{1/3}}$
フリードマン・ダイアコニスの選択（F-D’s choice）	$h = 2\frac{IQR(x)}{n^{1/3}}$

階級数（$k$）から階級幅（$h$）を求める場合は下式を使います。 \[h = \lceil \frac{max(x) - min(x)}{k} \rceil\] $k$ :階級の数
$h$ :階級の幅
$n$ :データの個数
$\lceil x \rceil$ :天井関数（実数$x$に対して$x$以上の最小の整数を返す関数）
$\sigma$ :標準偏差
$IQR$ :四分位範囲

数式出典：Wikipedia

スタージェスの公式

　スタージェスの公式は、比較的、よく使われる計算方法です。ただし、データの数が$30$個未満の場合には適切ではありませんし、データの数が多くなるとヒストグラムを平滑化し過ぎる傾向があると言われています。そのような傾向が見られた場合には、他の計算方法や任意の階級も試してみてください。

階級数をスタージェスの公式で求めた場合のヒストグラム

with(x, hist(height,
             breaks = "Sturges"))

スコットの選択

　スコットの選択は、データによってはスタージェスの公式と比べて階級数が少なくなる傾向があります。

階級数をスコットの選択を元に求めた場合のヒストグラム

with(x, hist(height, breaks = "Scott"))

フリードマン・ダイアコニスの選択

　フリードマン・ダイアコニスの法則とも呼ばれます。

階級数をフリードマン・ダイアコニスの選択を元に求めた場合のヒストグラム

with(x, hist(height, breaks = "FD"))

階級の境界の扱い

　階級は下表のように「下端値〜上端値」の形式で表示されることが多いですが、$140$は階級に含まれるのか？$145$はどちらの階級に含まれるのか？を決めておかないと意図しない度数になってしまう場合があります。

階級	度数
140〜145	1
145〜150	6
…	…
160〜165	16
165〜170	6

　例えば、階級を「$\mbox{下端値} < x \leq \mbox{上端値}$」と定義した場合は、下図のようになります。

階級の上端を含める場合のヒストグラム

with(x, hist(height, right = TRUE))

階級を「$\mbox{下端値} \leq x < \mbox{上端値}$」と定義した場合は、分布形状が異なることが分かります。

階級の下端を含める場合のヒストグラム

with(x, hist(height, right = FALSE))

　このように階級によりヒストグラムの形状が変わってくる点には注意が必要です。なお、下端、上端の含め方を「左閉じ、右閉じ」と表現することもあります。

等間隔ではない階級

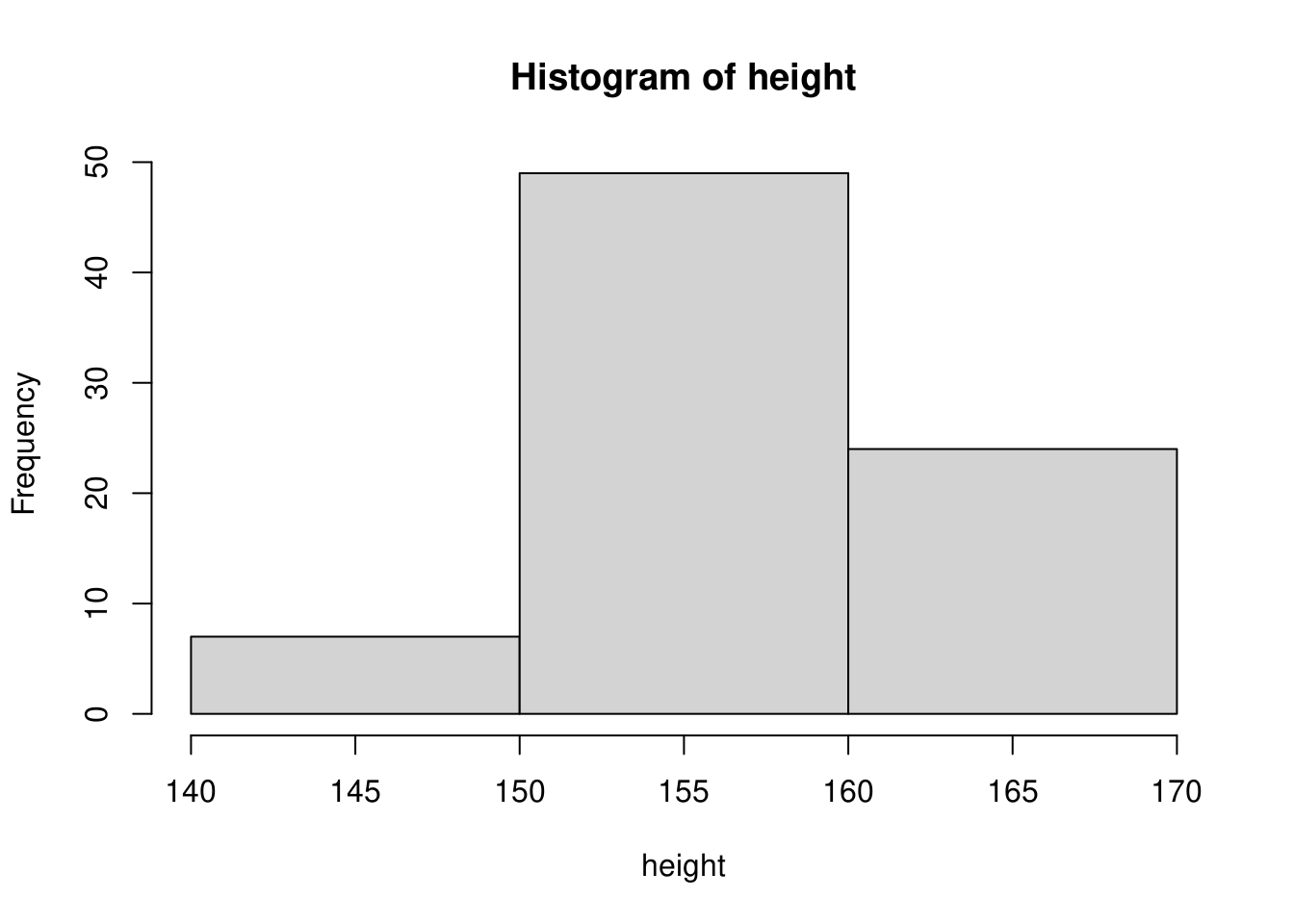
　度数分布表の階級は必ずしも等間隔である必要はありません。例えば、下図の世帯貯蓄のように度数の小さい階級をまとめたヒストグラムをしばしば見かけます。等間隔でないは階級は（最小値と最大値で桁が数桁異なるなど）幅が広いデータにおいて、階級を細かくしたい場合や等幅の階級でグラフ化するとデータを読み取りにくい場合などに使われます。

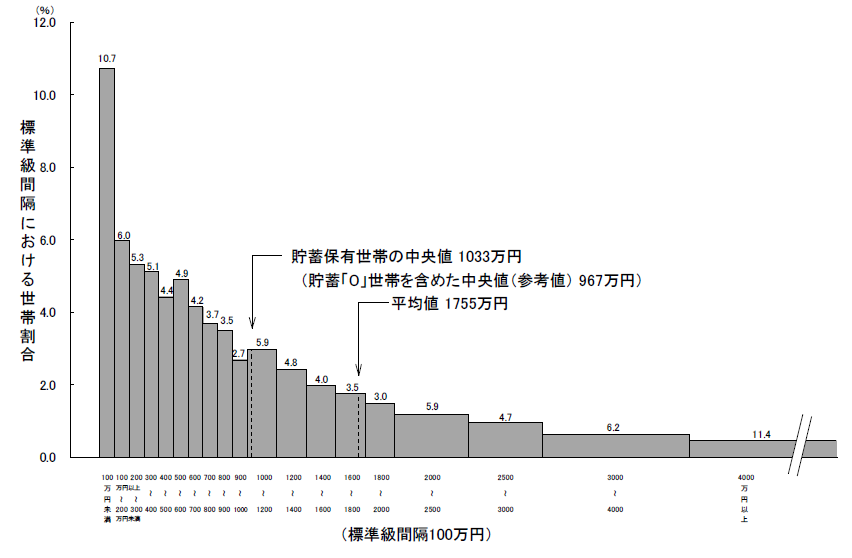（出典：なるほど統計学園）

　このように階級幅が等間隔でない場合には、柱（棒）の面積が度数に対応するように高さを調整する必要があります。
　ヒストグラムは棒グラフとは異なり階級ごとの柱（棒）の面積が意味を持っています。高さは一般的に度数として表示されますが、密度として表示することもあります。高さ（密度）と幅（階級幅）を乗じたものが相対度数になります。相対度数は名前の通り度数に比例していますので、柱（棒）の面積が等しければ同じ度数ということを表します。
　
　例えば、テキストにある身長のデータの$140cm$から$150cm$をひとつの階級にまとめた場合、度数分布表は下表のようになります。

等間隔ではない階級の度数分布表

x %>% 
  dplyr::mutate(class = cut(height,
                            breaks = c(140, 150,
                                       155, 160, 165, 170))) %>% 
  dplyr::count(class) %>% 
  dplyr::mutate(prop = prop.table(n)) %>% 
  dplyr::rename(`階級` = class, `度数` = n,
                `相対度数` = prop) %>% 
  df_print()

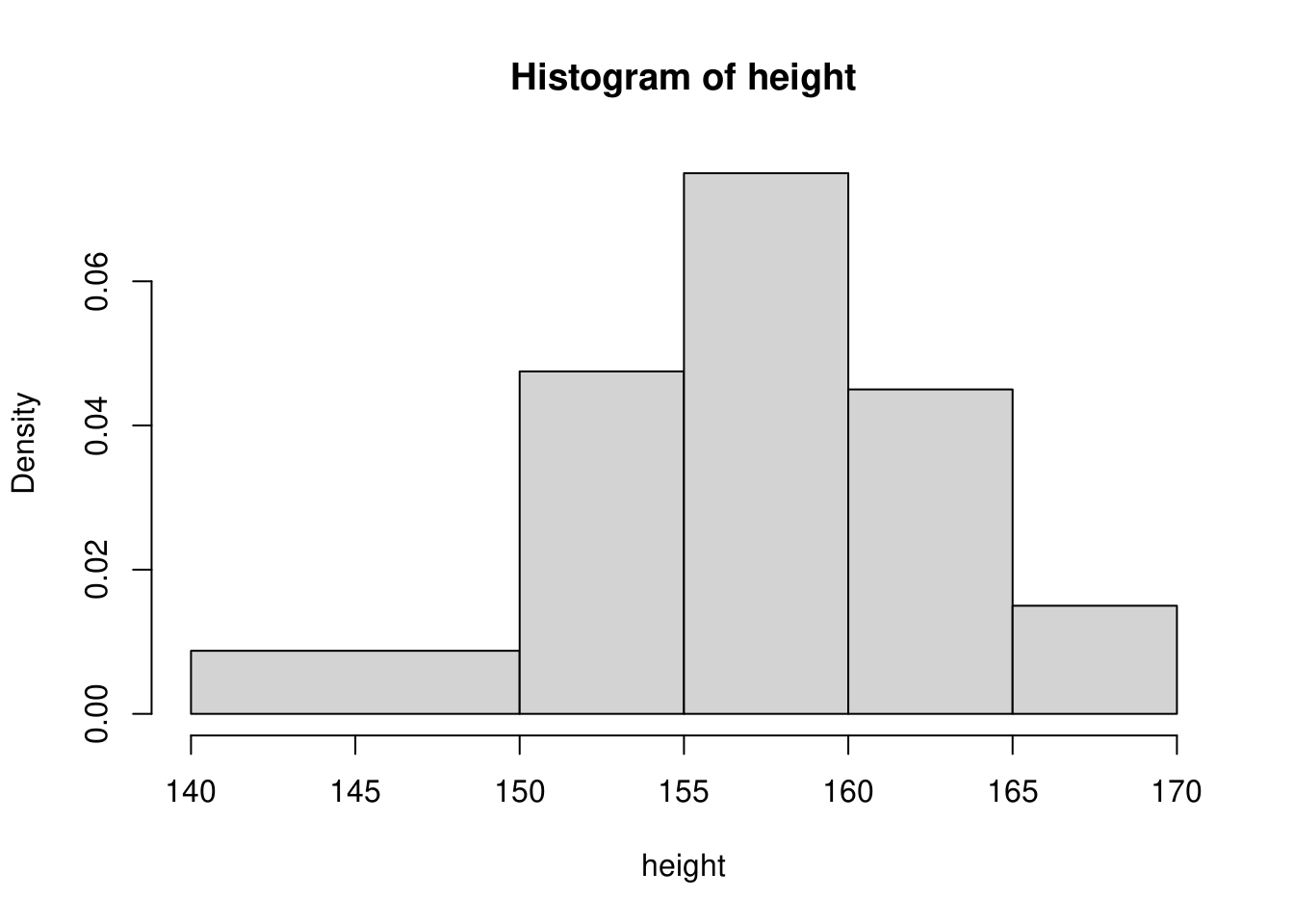
　これをヒストグラムとして描いた場合は、下図のようにならなければなりません。この図では縦軸は度数でなく密度になっています。

正しいヒストグラム

with(x, hist(height,
             breaks = c(140, 150, 155, 160, 165, 170)))

　密度（高さ）は左から
　　0.00875, 0.0475, 0.075, 0.045, 0.015
　となっていますので、これに個々の階級幅（幅）
　　10, 5, 5, 5, 5
　を乗じると個々の柱（棒）の面積は
　　0.0875, 0.2375, 0.375, 0.225, 0.075
　となり、相対度数と等しいことがわかります。　

　度数を表示させるために下図のようなヒストグラムを描くことは好ましくありません。階級幅が等幅でない場合は度数分布表と共に密度のヒストグラムを示した方がよいでしょう。

好ましくないヒストグラム（単なる棒グラフ）

with(x, hist(height,
             breaks = c(140, 150, 155, 160, 165, 170),
             freq = TRUE))

Warning in plot.histogram(r, freq = freq1, col = col, border = border, angle =
angle, : プロットの領域が誤まりです。むしろ 'freq = FALSE' を使用して下さい