7.1 最もよく見かけるデータ分布
図表7-1 標準正規分布のヒストグラム
# 「密度×階級幅=相対度数」の関係を用いて密度関数から相対度数を求める
data <- tibble::tibble(x = seq(-2.5, 2.5, 0.1),
y = dnorm(x) * 0.1)
data %>%
dplyr::mutate(y = dplyr::if_else(x == 0.0, y, 0)) %>%
ggplot2::ggplot(ggplot2::aes(x = x, y = y)) +
ggplot2::geom_bar(stat = "identity", data = data, alpha = 0.5,
fill = "deepskyblue1", colour = "deepskyblue3") +
ggplot2::geom_bar(stat = "identity", fill = "gray30") +
ggplot2::labs(x = "", y = "相対度数") +
ggplot2::scale_x_continuous(breaks = seq(-2.4, 2.4, 0.3)) +
ggplot2::scale_y_continuous(breaks = seq(0, 0.04, 0.005))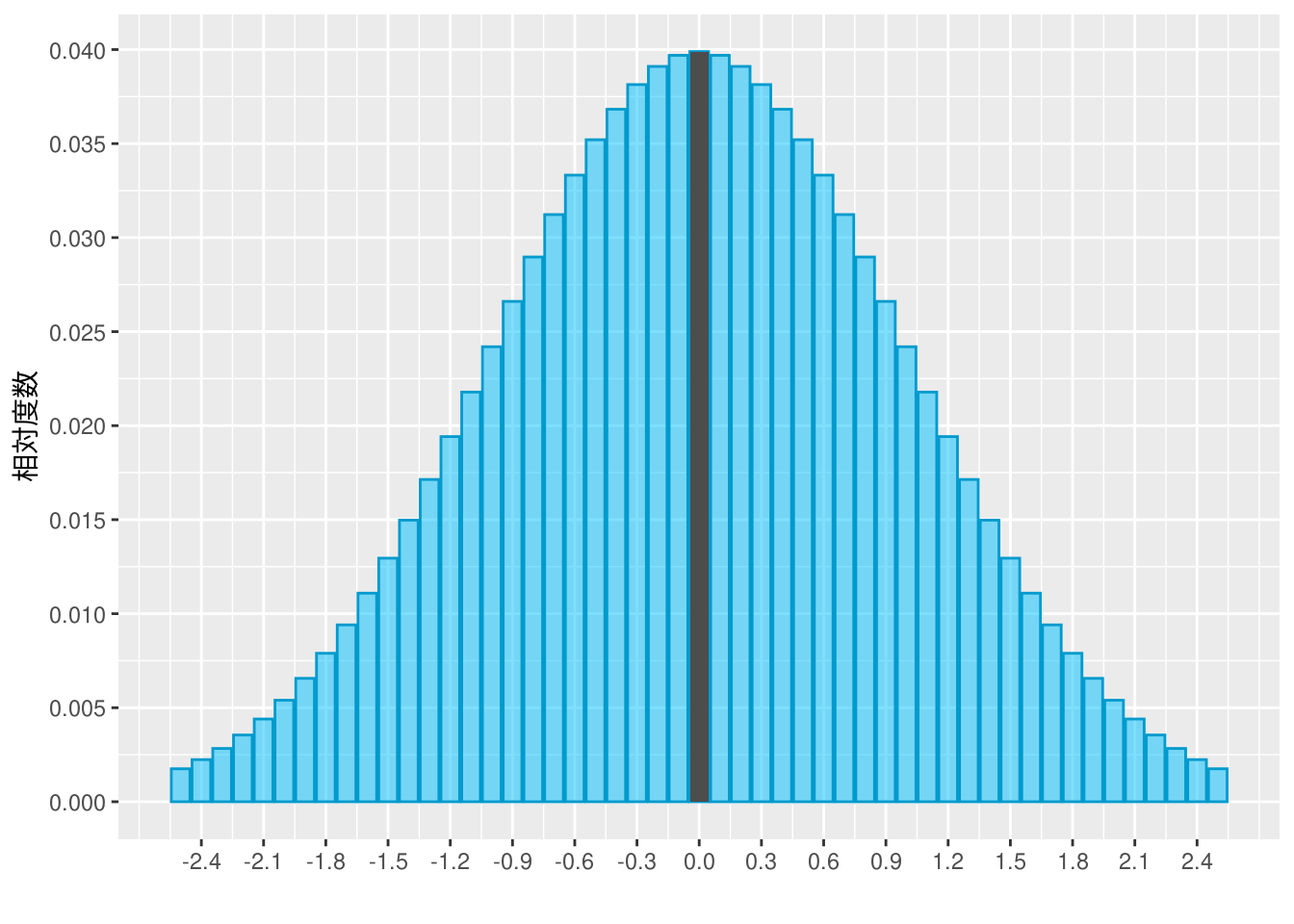
相対度数の総計は\(1\)ですので、相対度数を縦軸にして描いたヒストグラムの総面積は\(1\)になります。言い換えるヒストグラムの個々の柱(棒)の面積は相対度数と等しくなります。
一方、ヒストグラムは柱(棒)の面積が度数と等しくなるように描くのが一般的ですので、縦軸には相対度数でなく密度をとります。これにより\(\mbox{階級幅(幅)} \times \mbox{密度(高さ)} = \mbox{相対度数(面積)}\)の関係があることが分かります。
縦軸を密度にしたヒストグラム
tibble::tibble(x = seq(-2.5, 2.5, 0.1), y = dnorm(x)) %>%
ggplot2::ggplot(ggplot2::aes(x = x, y = y)) +
# ggplot2::geom_line(colour = "lightblue4") +
ggplot2::geom_bar(stat = "identity", alpha = 0.5,
fill = "deepskyblue1", colour = "deepskyblue3") +
ggplot2::labs(x = "", y = "密度") +
ggplot2::scale_x_continuous(breaks = seq(-2.4, 2.4, 0.3)) 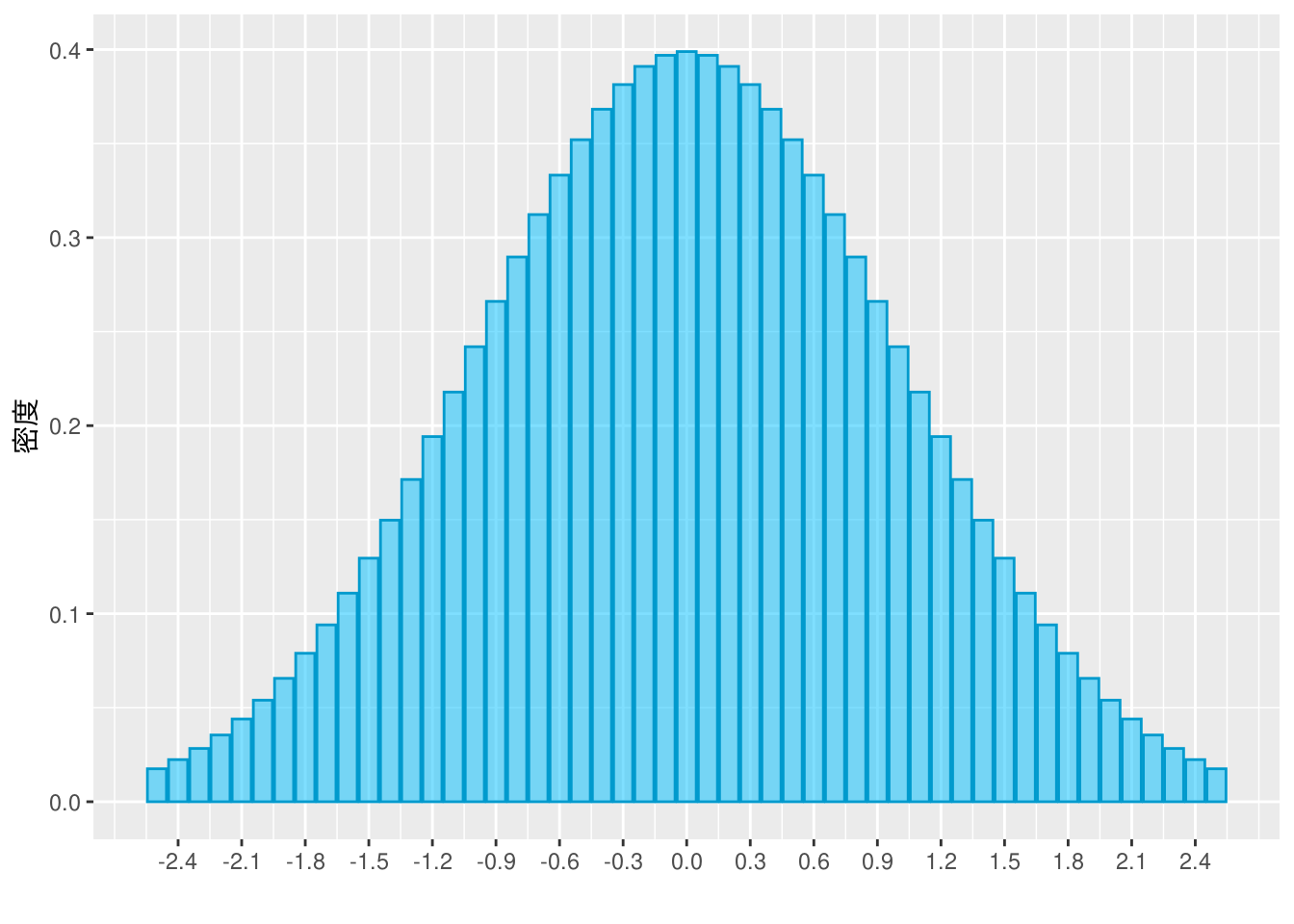
図表7-3 正規分布では標準偏差2個の範囲にほとんどのデータが入ってしまう
ddata2 <- tibble::tibble(x = seq(qnorm(0.160), qnorm(0.840), len = 101),
y = dnorm(x))
ddata3 <- tibble::tibble(x = seq(qnorm(0.025), qnorm(0.975), len = 101),
y = dnorm(x))
tibble::tibble(x = seq(-4, 4, len = 101), y = dnorm(x)) %>%
ggplot2::ggplot(ggplot2::aes(x, y)) +
ggplot2::geom_line(size = 0.25) +
ggplot2::geom_ribbon(ggplot2::aes(x, y, ymin = 0, ymax = y),
data = ddata3, fill = "deepskyblue1", alpha = 0.75) +
ggplot2::geom_ribbon(ggplot2::aes(x, y, ymin = 0, ymax = y),
data = ddata2, fill = "deepskyblue3", alpha = 0.75) +
ggplot2::scale_x_continuous(breaks = seq(-3, 3, 1)) +
ggplot2::theme(axis.title = ggplot2::element_blank(),
axis.text.y = ggplot2::element_blank(),
axis.ticks.y = ggplot2::element_blank())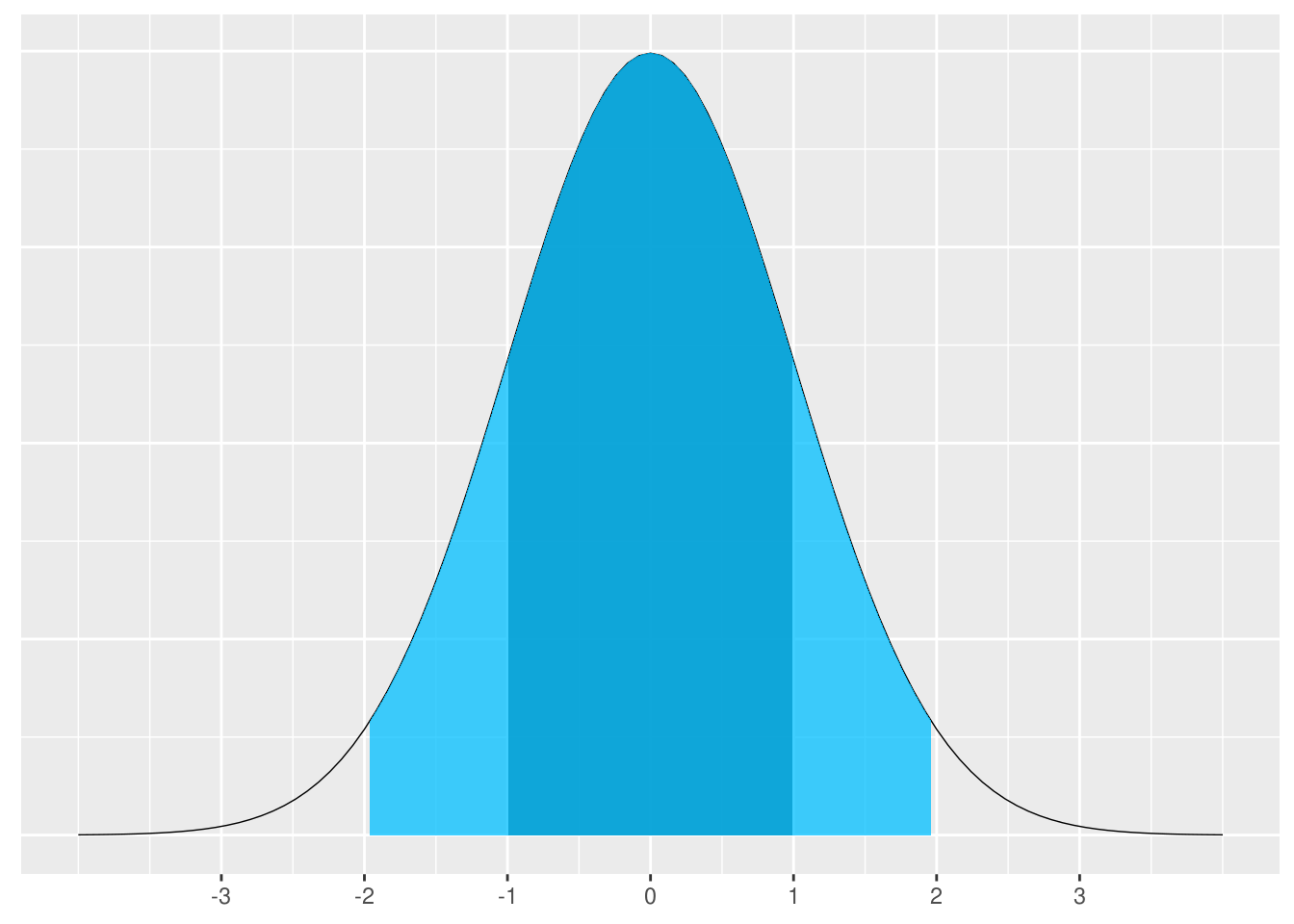
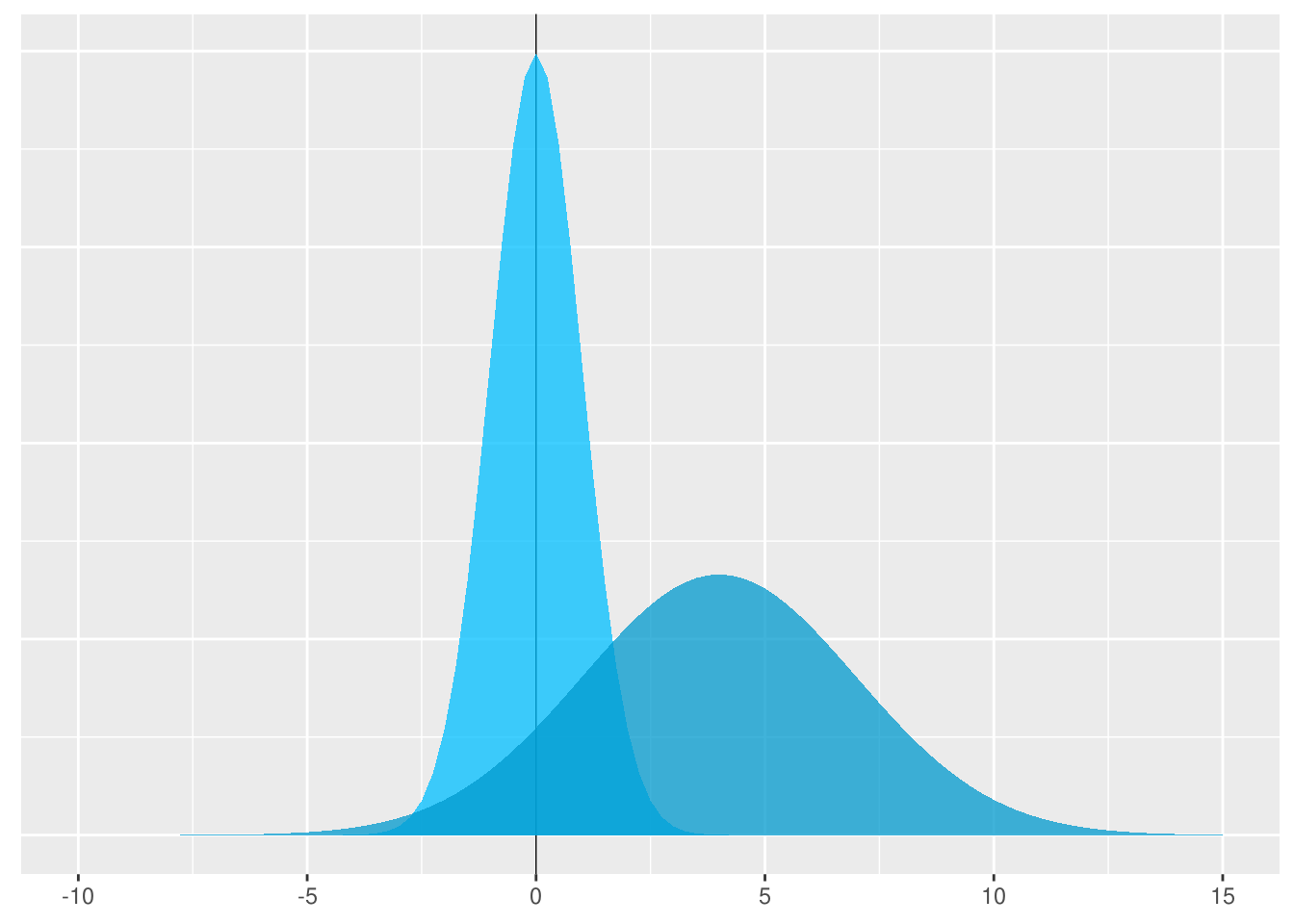
図表7-4 標準正規分布でから一般正規分布へ
ndata1 <- tibble::tibble(x = seq(-10, 15, len = 101),
y = dnorm(x, mean = 0, sd = 1))
ndata2 <- tibble::tibble(x = seq(-10, 15, len = 101),
y = dnorm(x, mean = 4, sd = 3))
ggplot2::ggplot() +
ggplot2::geom_vline(xintercept = 0, size = 0.25) +
ggplot2::geom_ribbon(ggplot2::aes(x, y, ymin = 0, ymax = y), data = ndata1,
fill = "deepskyblue1", alpha = 0.75) +
ggplot2::geom_ribbon(ggplot2::aes(x, y, ymin = 0, ymax = y), data = ndata2,
fill = "deepskyblue3", alpha = 0.75) +
ggplot2::theme(axis.title = ggplot2::element_blank(),
axis.text.y = ggplot2::element_blank(),
axis.ticks.y = ggplot2::element_blank())